题目内容
已知x2-6x+8y+y2+25=0,求2x-3y的值.
考点:配方法的应用,非负数的性质:偶次方
专题:计算题
分析:利用配方法把已知条件变形为(x-3)2+(y+4)2=0,则根据非负数的性质得x-3=0,y+4=0,然后求出x和y的值后再计算2x-4y.
解答:解:∵x2-6x+8y+y2+25=0,
∴x2-6x+9+y2+8y+16=0,
∴(x-3)2+(y+4)2=0,
∴x-3=0,y+4=0,
∴x=3,y=-4,
∴2x-3y=2×3-3×(-4)=18.
∴x2-6x+9+y2+8y+16=0,
∴(x-3)2+(y+4)2=0,
∴x-3=0,y+4=0,
∴x=3,y=-4,
∴2x-3y=2×3-3×(-4)=18.
点评:本题考查了配方法的应用:用配方法解一元二次方程;利用配方法求二次三项式是一个完全平方式时所含字母系数的值.也考查了非负数的性质.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
桌上摆满了朋友们送来的礼物,小狗贝贝好奇地想看个究竟.①小狗先是站在地面上看,②然后抬起了前腿看,③唉,还是站到凳子上看吧,④最后,它终于爬上了桌子…请你根据小狗四次看礼物的顺序,把图乙四副图片按对应字母正确排序为( )
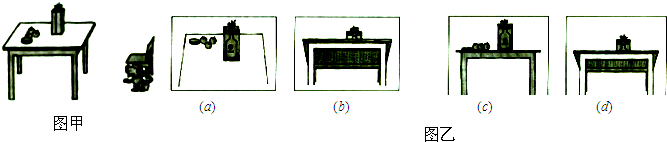

| A、(a) (b) (c) (d) |
| B、(c) (b) (d) (a) |
| C、(b) (a) (c) (d) |
| D、(b) (d) (c) (a) |
 如图,已知NG平分∠BNF,∠AMD=∠MNF,∠CMN:∠DMN=3:5,试求∠MNF和∠GNF的度数.
如图,已知NG平分∠BNF,∠AMD=∠MNF,∠CMN:∠DMN=3:5,试求∠MNF和∠GNF的度数. 如图,在△ABC中,AC=AB,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,求△BCF的周长和∠EFC的度数.
如图,在△ABC中,AC=AB,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,求△BCF的周长和∠EFC的度数. (1)已知;△ABC中,BD、CE是∠B、∠C的角平分线,并交于点O.求证:∠BOC=90°+
(1)已知;△ABC中,BD、CE是∠B、∠C的角平分线,并交于点O.求证:∠BOC=90°+