题目内容
15.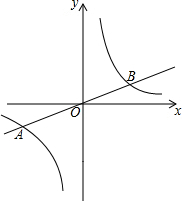 如图,在平面直角坐标系xOy中,已知正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$的图象交于A(a,-2),B两点.
如图,在平面直角坐标系xOy中,已知正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$的图象交于A(a,-2),B两点.(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.
分析 (1)把A(a,-2)代入y=$\frac{1}{2}$x,可得A(-4,-2),把A(-4,-2)代入y=$\frac{k}{x}$,可得反比例函数的表达式为y=$\frac{8}{x}$,再根据点B与点A关于原点对称,即可得到B的坐标;
(2)过P作PE⊥x轴于E,交AB于C,先设P(m,$\frac{8}{m}$),则C(m,$\frac{1}{2}$m),根据△POC的面积为3,可得方程$\frac{1}{2}$m×|$\frac{1}{2}$m-$\frac{8}{m}$|=3,求得m的值,即可得到点P的坐标.
解答 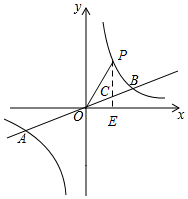 解:(1)把A(a,-2)代入y=$\frac{1}{2}$x,可得a=-4,
解:(1)把A(a,-2)代入y=$\frac{1}{2}$x,可得a=-4,
∴A(-4,-2),
把A(-4,-2)代入y=$\frac{k}{x}$,可得k=8,
∴反比例函数的表达式为y=$\frac{8}{x}$,
∵点B与点A关于原点对称,
∴B(4,2);
(2)如图所示,过P作PE⊥x轴于E,交AB于C,
设P(m,$\frac{8}{m}$),则C(m,$\frac{1}{2}$m),
∵△POC的面积为3,
∴$\frac{1}{2}$m×|$\frac{1}{2}$m-$\frac{8}{m}$|=3,
解得m=2$\sqrt{7}$或2,
∴P(2$\sqrt{7}$,$\frac{4}{7}\sqrt{7}$)或(2,4).
点评 本题主要考查了反比例函数与一次函数的交点问题,解题时注意:反比例函数与一次函数的图象的交点坐标满足两函数的解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若△ABC~△DEF,相似比为3:2,则对应高的比为( )
| A. | 3:2 | B. | 3:5 | C. | 9:4 | D. | 4:9 |
20.生物学家发现了一种病毒,其长度约为0.00000032mm,数据0.00000032用科学记数法表示正确的是( )
| A. | 3.2×107 | B. | 3.2×108 | C. | 3.2×10-7 | D. | 3.2×10-8 |
5.下列图案

其中,中心对称图形是( )

其中,中心对称图形是( )
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
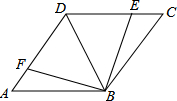 如图,点E,F分别在菱形ABCD的边DC,DA上,且CE=AF.
如图,点E,F分别在菱形ABCD的边DC,DA上,且CE=AF. 如图所示的几何体是由4个大小相同的小立方体组成,其俯视图是( )
如图所示的几何体是由4个大小相同的小立方体组成,其俯视图是( )


