题目内容
1.关于x的一元二次方程x2-(2m+1)x+(m2+2)=0的两个实数根分别是x1、x2,且x12+x22=13,则(x1-x2)2的值是( )| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
分析 根据根的判别式的意义得到m≥$\frac{7}{4}$,再根据根与系数的关系得到x1+x2=2m+1,x1x2=m2+2,由x12+x22=13可得(2m+1)2-2(m2+2)=13,解得m1=2,m2=-4,由于m≥$\frac{7}{4}$,所以m=2,则x1+x2=5,x1x2=6,然后根据完全平方公式得到(x1-x2)2=(x1+x2)2-4x1x2,再利用整体代入的方法计算.
解答 解:根据题意得△=(2m+1)2-4(m2+2)≥0,解得m≥$\frac{7}{4}$,
x1+x2=2m+1,x1x2=m2+2,
∵x12+x22=13,
∴(x1+x2)2-2x1x2=13,
∴(2m+1)2-2(m2+2)=13,
整理得m2+2m-8=0,解得m1=2,m2=-4,
而m≥$\frac{7}{4}$,
∴m=2,
∴x1+x2=5,x1x2=6,
∴(x1-x2)2=(x1+x2)2-4x1x2=52-4×6=1.
故选C.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
相关题目
12.一个多边形的内角和是1620°,那么这个多边形是( )
| A. | 八边形 | B. | 九边形 | C. | 十边形 | D. | 十一边形 |
9.如果把多边形的边数增加一倍.得到的新多边形的内角和是1440°,那么原来多边形的边数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
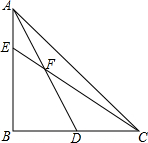 已知:△ABC中,AD是BC边中线,E是AB上一点,CE交直线AD于F,若CF=AB,求证:AE=EF.
已知:△ABC中,AD是BC边中线,E是AB上一点,CE交直线AD于F,若CF=AB,求证:AE=EF.