题目内容
 有理数a、b、c在数轴上的位置如图:
有理数a、b、c在数轴上的位置如图:(1)判断正负,用“>”或“<”填空:b-c
a+b
(2)化简:|b-c|+|a+b|-|c-a|.
考点:绝对值,数轴
专题:
分析:(1)根据数轴判断出a、b、c的正负情况,然后分别判断即可;
(2)去掉绝对值号,然后合并同类项即可.
(2)去掉绝对值号,然后合并同类项即可.
解答:解:(1)由图可知,a<0,b>0,c>0且|b|<|a|<|c|,
所以,b-c<0,a+b<0,c-a>0;
故答案为:<,<,>;
(2)|b-c|+|a+b|-|c-a|
=(c-b)+(-a-b)-(c-a)
=c-b-a-b-c+a
=-2b.
所以,b-c<0,a+b<0,c-a>0;
故答案为:<,<,>;
(2)|b-c|+|a+b|-|c-a|
=(c-b)+(-a-b)-(c-a)
=c-b-a-b-c+a
=-2b.
点评:本题考查了绝对值的性质,数轴,熟记性质并准确识图观察出a、b、c的正负情况是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
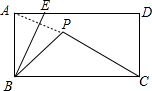 如图所示,长方形ABCD中,AB=4,BC=8,点E是折线段A-D-C上的一个动点,点P是点A关于BE的对称点,在点E运动的过程中,能使△PCB为等腰三角形的点E的位置共有( )个.
如图所示,长方形ABCD中,AB=4,BC=8,点E是折线段A-D-C上的一个动点,点P是点A关于BE的对称点,在点E运动的过程中,能使△PCB为等腰三角形的点E的位置共有( )个.| A、2个 | B、3个 | C、4个 | D、5个 |
已知△ABC的三个顶点都在⊙O上,AB=AC,⊙O的半径等于5cm,圆心O到BC的距离为3cm,则AB的长等于( )
A、2
| ||||
B、2
| ||||
C、4
| ||||
D、2
|
下列合并同类项正确的是( )
| A、3x+y=4xy |
| B、2x2+3x2=5x4 |
| C、6x2-3x2=3 |
| D、5xy-3xy=2xy |
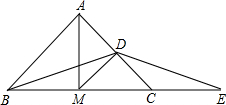 已知△ABC中,AB=AC=5,BC=6,AM平分∠BAC,D为AC的中点,E为BC延长线上一点,且CE=
已知△ABC中,AB=AC=5,BC=6,AM平分∠BAC,D为AC的中点,E为BC延长线上一点,且CE=