题目内容
已知△ABC的三个顶点都在⊙O上，AB=AC，⊙O的半径等于5cm，圆心O到BC的距离为3cm，则AB的长等于（ ）
A、2
| ||||
B、2
| ||||
C、4
| ||||
D、2
|
考点：垂径定理,等腰三角形的性质,勾股定理
专题：
分析：此题分情况考虑：当三角形的外心在三角形的内部时，根据勾股定理求得BD的长，再根据勾股定理求得AB的长；当三角形的外心在三角形的外部时，根据勾股定理求得BD的长，再根据勾股定理求得AB的长．
解答：
解：如图1，当△ABC是锐角三角形时，连接AO并延长到BC于点D，
∵AB=AC，O为外心，
∴AD⊥BC，
在Rt△BOD中，
∵OB=5，OD=3，
∴BD=
=
=4．
在Rt△ABD中，根据勾股定理，得AB=
=4
（cm）；
当当△ABC是钝角或直角三角形时，如图2所示，连接AO交BC于点D，
在Rt△BOD中，
∵OB=5，OD=3，
∴BD=
=
=4，
∴AD=5-3=2，
在Rt△ABD中，根据勾股定理，得AB=
=
=2
（cm）．
故选D．
解：如图1，当△ABC是锐角三角形时，连接AO并延长到BC于点D，∵AB=AC，O为外心，
∴AD⊥BC，
在Rt△BOD中，
∵OB=5，OD=3，
∴BD=
| OB2-OD2 |
| 52-32 |
在Rt△ABD中，根据勾股定理，得AB=
| 42+82 |
| 5 |
当当△ABC是钝角或直角三角形时，如图2所示，连接AO交BC于点D，
在Rt△BOD中，
∵OB=5，OD=3，
∴BD=
| OB2-OD2 |
| 52-32 |
∴AD=5-3=2，
在Rt△ABD中，根据勾股定理，得AB=
| BD2+AD2 |
| 16+4 |
| 5 |
故选D．
点评：本题考查的是垂径定理，在解答此题时要注意进行分类讨论，不要漏解．
练习册系列答案
阅读快车系列答案
相关题目
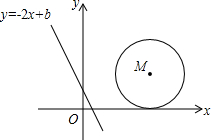如图，在平面直角坐标系中，直线l：y=-2x+b（b≥0）的位置随b的不同取值而变化，已知⊙M的圆心坐标为（3，2），半径为2，当b=
有理数a，b在数轴的位置如图，则下面关系中正确的个数为（ ）
有理数a、b、c在数轴上的位置如图：
下面几何体的三种视图有无错误？如果有，请改正．