题目内容
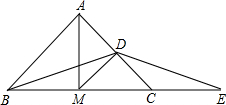 已知△ABC中,AB=AC=5,BC=6,AM平分∠BAC,D为AC的中点,E为BC延长线上一点,且CE=
已知△ABC中,AB=AC=5,BC=6,AM平分∠BAC,D为AC的中点,E为BC延长线上一点,且CE=| 1 |
| 2 |
(1)求ME的长;
(2)求证:DB=DE.
考点:等腰三角形的判定与性质,直角三角形斜边上的中线
专题:
分析:(1)由条件可知M是BC的中点,可知BM=CM=CE=3;
(2)由条件可知DM为Rt△AMC斜边上的中线,可得DM=DC=2.5,过D作DN⊥MC于点N,则可求得BN=EN,可得DB=DE.
(2)由条件可知DM为Rt△AMC斜边上的中线,可得DM=DC=2.5,过D作DN⊥MC于点N,则可求得BN=EN,可得DB=DE.
解答:(1)解:∵AB=AC=5,AM平分∠BAC,
∴BM=CM=
BC=CE=3,
∴ME=MC+CE=3+3=6;
(2)证明:∵AB=AC=5,AM平分∠BAC,
∴AM⊥BC,且D为AC中点,
∴DM=DC,
过D作DN⊥MC,如图,则MN=CN,

又∵BM=CE,
∴BN=EN,
∴D在线段BE的垂直平方线上,
∴DB=DE.
∴BM=CM=
| 1 |
| 2 |
∴ME=MC+CE=3+3=6;
(2)证明:∵AB=AC=5,AM平分∠BAC,
∴AM⊥BC,且D为AC中点,
∴DM=DC,
过D作DN⊥MC,如图,则MN=CN,

又∵BM=CE,
∴BN=EN,
∴D在线段BE的垂直平方线上,
∴DB=DE.
点评:本题主要考查等腰三角形的判定和性质及直角三角形的性质,由条件得到M为BC的中点及AM⊥BC是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
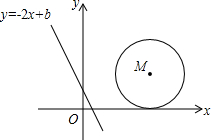 如图,在平面直角坐标系中,直线l:y=-2x+b(b≥0)的位置随b的不同取值而变化,已知⊙M的圆心坐标为(3,2),半径为2,当b=
如图,在平面直角坐标系中,直线l:y=-2x+b(b≥0)的位置随b的不同取值而变化,已知⊙M的圆心坐标为(3,2),半径为2,当b= 有理数a、b、c在数轴上的位置如图:
有理数a、b、c在数轴上的位置如图: