题目内容
18. 已知在正方形ABCD中,CE=3DE,AF⊥BE,求sin∠BAF的值.
已知在正方形ABCD中,CE=3DE,AF⊥BE,求sin∠BAF的值.
分析 设正方形的边长为4a,则CE=3a,在△BCE中,先利用勾股定理计算出BE=5a,再利用正弦的定义得到sin∠CBE=$\frac{3}{5}$,然后根据等角的余角相等得到∠ABF=∠CBE,于是有sin∠BAF=$\frac{3}{5}$.
解答 解:设正方形的边长为4a,则BC=CD=4a,
∵CE=3DE,
∴CE=3a,
在△BCE中,BE=$\sqrt{B{C}^{2}+C{E}^{2}}$=$\sqrt{(4a)^{2}+(3a)^{2}}$=5a,
∴sin∠CBE=$\frac{CE}{BE}$=$\frac{3a}{5a}$=$\frac{3}{5}$,
∵AF⊥BE,
∴∠BAF+∠ABF=90°,
∵∠CBE+∠ABF=90°,
∴∠ABF=∠CBE,
∴sin∠BAF=$\frac{3}{5}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活应用勾股定理和三角函数的定义进行计算.

练习册系列答案
相关题目
 如图,已知C是线段AB上的一点,M,N分别是AC,BC的中点.
如图,已知C是线段AB上的一点,M,N分别是AC,BC的中点.
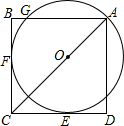 如图.圆心O在边长为2$\sqrt{2}$的正方形ABCD的对角线AC上,⊙O过点A,且BC,CD都相切,求$\widehat{AG}$的长.
如图.圆心O在边长为2$\sqrt{2}$的正方形ABCD的对角线AC上,⊙O过点A,且BC,CD都相切,求$\widehat{AG}$的长. 如图,小明在A点用测倾仪测得旗杆顶端E的仰角为69°,测倾仪的高度CA为1.55m,点A到旗杆底部B的距离为11.7m.求旗杆BE的高度(精确到1m)
如图,小明在A点用测倾仪测得旗杆顶端E的仰角为69°,测倾仪的高度CA为1.55m,点A到旗杆底部B的距离为11.7m.求旗杆BE的高度(精确到1m)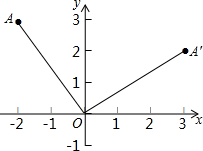 如图,点A坐标为(-2,3),将点A绕原点O顺时针旋转90°得点A′,求A′的坐标.
如图,点A坐标为(-2,3),将点A绕原点O顺时针旋转90°得点A′,求A′的坐标.