题目内容
16.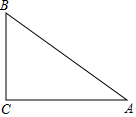 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D,E分别在边AB,AC上,将△ADE沿直线DE翻折,点A的对应点在边AB上,联结A′C,如果A′C=A′A,那么BD=$\frac{15}{2}$.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D,E分别在边AB,AC上,将△ADE沿直线DE翻折,点A的对应点在边AB上,联结A′C,如果A′C=A′A,那么BD=$\frac{15}{2}$.
分析 根据勾股定理得到AB=10,根据等腰三角形的性质得到∠A=∠A′CA,根据余角的性质得到∠B=∠BCA′,得到AA′=A′B=$\frac{1}{2}$AB=5,根据折叠的性质得到A′D=AD=$\frac{5}{2}$,于是得到结论.
解答 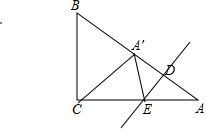 解:∵在Rt△ABC中,∠C=90°,AC=8,BC=6,
解:∵在Rt△ABC中,∠C=90°,AC=8,BC=6,
∴AB=10,
∵A′C=A′A,
∴∠A=∠A′CA,
∵∠ACB=90°,
∴∠B+∠A=∠BCA′+∠A′CA=90°,
∴∠B=∠BCA′,
∴AA′=A′B=$\frac{1}{2}$AB=5,
∵将△ADE沿直线DE翻折,
∴A′D=AD=$\frac{5}{2}$,
∴BD=A′B+A′D=$\frac{15}{2}$,
故答案为:$\frac{15}{2}$.
点评 本题考查了翻折变换的性质、线段垂直平分线的性质、勾股定理、等腰三角形的性质;本题有一定难度.

练习册系列答案
相关题目
11.以一个面积为1的三角形的三条中位线为三边的三角形的面积为( )
| A. | 4 | B. | 2 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
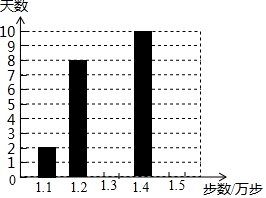 乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).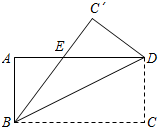 把矩形ABCD沿着对角线BD折叠,使点C落在C′处,交AD于E,若AD=8,AB=4,则AE的长为( )
把矩形ABCD沿着对角线BD折叠,使点C落在C′处,交AD于E,若AD=8,AB=4,则AE的长为( ) 如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.
如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.