题目内容
点A(
,b)是抛物线y=x2上的一点,则b= ;过点A作x轴的平行线交抛物线另一点B的坐标是 .
| 1 |
| 2 |
考点:二次函数图象上点的坐标特征
专题:
分析:利用待定系数法把A(
,b)代入y=x2可得b的值,进而得到A点坐标,再根据函数解析式可得y=x2的对称轴是y轴,因此过点A作x轴的平行线交抛物线另一点B与A关于y轴对称,进而可得答案.
| 1 |
| 2 |
解答:解:把A(
,b)代入y=x2得:b=
,
∵y=x2的对称轴是y轴,
∴过点A作x轴的平行线交抛物线另一点B的坐标是(-
,
),
故答案为:
;(-
,
).
| 1 |
| 2 |
| 1 |
| 4 |
∵y=x2的对称轴是y轴,
∴过点A作x轴的平行线交抛物线另一点B的坐标是(-
| 1 |
| 2 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:此题主要考查了二次函数图象上点的坐标特点,以及二次函数图象的对称轴,关键是掌握y=x2的对称轴是y轴.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
点A的坐标是(1,1),若点B在坐标轴上,且△ABO是等腰三角形,则点B的坐标不可能是( )
| A、(2,0) |
| B、(0.5,0) |
| C、(1,0) |
| D、(0,1) |
 已知抛物线y=-
已知抛物线y=- 如图,四边形ABCD是正方形,以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE,猜想如图中线段BG、线段DE的关系并证明.
如图,四边形ABCD是正方形,以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE,猜想如图中线段BG、线段DE的关系并证明.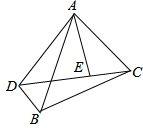 如图,△ADE与△ABC有公共顶点A,∠BAD=∠CAE.
如图,△ADE与△ABC有公共顶点A,∠BAD=∠CAE.