题目内容
 如图,四边形ABCD是正方形,以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE,猜想如图中线段BG、线段DE的关系并证明.
如图,四边形ABCD是正方形,以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE,猜想如图中线段BG、线段DE的关系并证明.考点:正方形的性质,全等三角形的判定与性质
专题:
分析:根据正方形的性质可得BC=CD,CG=CE,∠BCD=∠ECG=90°,然后求出∠BCG=∠DCE,再利用“边角边”证明△BCG和△DCE全等,根据全等三角形对应角相等可得BG=DE,全等三角形对应角相等可得∠CBG=∠CDE,再求出∠DOH=90°,根据垂直的定义证明即可.
解答:解:BG=DE,BG⊥DE;.
证明如下:∵四边形ABCD、四边形CEFG都是正方形,
∴BC=CD,CG=CE,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE,
在△BCG和△DCE中,
,
∴△BCG≌△DCE(SAS),
∴BG=DE,∠CBG=∠CDE,
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,
∴∠CDE+∠DHO=90°,
∴∠DOH=90°,
∴BG⊥DE.
证明如下:∵四边形ABCD、四边形CEFG都是正方形,
∴BC=CD,CG=CE,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE,
在△BCG和△DCE中,
|
∴△BCG≌△DCE(SAS),
∴BG=DE,∠CBG=∠CDE,
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,
∴∠CDE+∠DHO=90°,
∴∠DOH=90°,
∴BG⊥DE.
点评:本题考查了正方形的性质,全等三角形的判定与性质,三角形的内角和定理,熟记各性质并求出三角形全等是解题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
已知
-1的整数部分为a,小数部分为b,则(
+a)(b+1)=( )
| 11 |
| 11 |
| A、5 | B、6 | C、7 | D、8 |
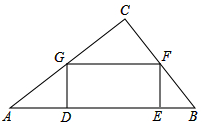 内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上.
内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上. 如图,在△ABC中,AB=2014,AC=2012,AD为中线,则△ABD与△ACD的周长之差为
如图,在△ABC中,AB=2014,AC=2012,AD为中线,则△ABD与△ACD的周长之差为