题目内容
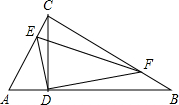 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,E、F分别是AC、BC边上的点,且CE=
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,E、F分别是AC、BC边上的点,且CE=| 1 |
| 3 |
| 1 |
| 3 |
(1)
| AC |
| BC |
| CD |
| BD |
(2)∠BDC=∠FDB.
考点:相似三角形的判定与性质
专题:证明题
分析:(1)证相关线段所在的三角形相似即可,即证Rt△ADC∽Rt△CDB;
(2)易证得CE:BF=AC:BC,联立(1)的结论,即可得出CE:BF=CD:BD,由此易证得△CED∽△BFD,即可得出∠CDE=∠BDF.
(2)易证得CE:BF=AC:BC,联立(1)的结论,即可得出CE:BF=CD:BD,由此易证得△CED∽△BFD,即可得出∠CDE=∠BDF.
解答:证明:(1)∵∠ACB=90°,CD⊥AB,
∴∠CDB=∠ACB=90°,
又∵∠B=∠B,
∴△ACB∽△CDB,
∴
=
;
(2)∵CE=
AC,BF=
BC,
∴CE:BF=AC:BC,
∴由(1)的结论得:CE:BF=CD:BD,
∵∠B+∠BCD=∠ECD+∠BCD=90°,
∴∠B=∠ECD,
∴△ECD∽△FBD.
∴∠EDC=∠FDB.
∴∠CDB=∠ACB=90°,
又∵∠B=∠B,
∴△ACB∽△CDB,
∴
| AC |
| BC |
| CD |
| BD |
(2)∵CE=
| 1 |
| 3 |
| 1 |
| 3 |
∴CE:BF=AC:BC,
∴由(1)的结论得:CE:BF=CD:BD,
∵∠B+∠BCD=∠ECD+∠BCD=90°,
∴∠B=∠ECD,
∴△ECD∽△FBD.
∴∠EDC=∠FDB.
点评:此题考查的是相似三角形的判定和性质;识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
下列四个汽车标志图中,中心对称图形是( )
A、 |
B、 |
C、 |
D、 |
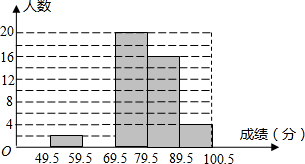 某校数学兴趣小组成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图和频数、频率分布表.请你根据图表提供的信息,解答下列问题:
某校数学兴趣小组成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图和频数、频率分布表.请你根据图表提供的信息,解答下列问题: 如图,在?ABCD中,AC、BD相交于点O,AB⊥AC,AB=AC=2,求BD的长.
如图,在?ABCD中,AC、BD相交于点O,AB⊥AC,AB=AC=2,求BD的长.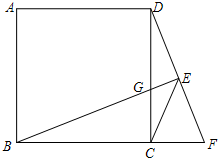 如图,在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.
如图,在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE. 已知△A′B′C′是由△ABC向上平移2个单位长度,再向右平移4个单位长度得到的,已知△ABC各顶点在平面直角坐标系中的坐标为:A(-1,0),B(3,-1),C(5,4).
已知△A′B′C′是由△ABC向上平移2个单位长度,再向右平移4个单位长度得到的,已知△ABC各顶点在平面直角坐标系中的坐标为:A(-1,0),B(3,-1),C(5,4).