题目内容
平面直角坐标系内AB∥x轴,AB=5,点A的坐标为(2,-3),则点B的坐标为 .
考点:坐标与图形性质
专题:
分析:根据平行于x轴的直线是上的点的纵坐标相等求出点B的纵坐标,再分点B在点A的左边与右边两种情况求出点B的横坐标,即可得解.
解答:解:∵AB∥x轴,点A的坐标为(2,-3),
∴点B的横坐标为-3,
∵AB=5,
∴点B在点A的左边时,横坐标为2-5=-3,
点B在点A的右边时,横坐标为2+5=7,
∴点B的坐标为(-3,-3)或(7,-3).
故答案为:(-3,-3)或(7,-3).
∴点B的横坐标为-3,
∵AB=5,
∴点B在点A的左边时,横坐标为2-5=-3,
点B在点A的右边时,横坐标为2+5=7,
∴点B的坐标为(-3,-3)或(7,-3).
故答案为:(-3,-3)或(7,-3).
点评:本题考查了坐标与图形性质,主要利用了平行于x轴的直线是上的点的纵坐标相等的性质,难点在于要分情况讨论.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
已知关于x的一元二次方程(a-2)x2-x+a2-4=0的一个根是0,那么a的值为( )
| A、a=0 | B、a=2 |
| C、a=-2 | D、a=2或-2 |
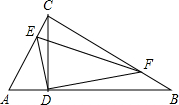 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,E、F分别是AC、BC边上的点,且CE=
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,E、F分别是AC、BC边上的点,且CE= 如图,把一个长方形纸片对折两次,然后剪下一个角,为了得到一个正方形,剪刀与折痕所成的角为
如图,把一个长方形纸片对折两次,然后剪下一个角,为了得到一个正方形,剪刀与折痕所成的角为