题目内容
解方程
(1)x2-x-20=0
(2)(x-2)2=3(x-2)
(3)2x2-4x-9=0(用配方法解)
(1)x2-x-20=0
(2)(x-2)2=3(x-2)
(3)2x2-4x-9=0(用配方法解)
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:计算题
分析:(1)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(2)方程移项后,提取公因式化为积的形式,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(3)方程二次项系数化为1,常数项移到右边,两边加上一次项系数一半的平方,利用完全平方公式变形后,开方即可求出解.
(2)方程移项后,提取公因式化为积的形式,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(3)方程二次项系数化为1,常数项移到右边,两边加上一次项系数一半的平方,利用完全平方公式变形后,开方即可求出解.
解答:解:(1)分解因式得:(x-5)(x+4)=0,
解得:x1=5,x2=-4;
(2)方程变形得:(x-2)2-3(x-2)=0,
分解因式得:(x-2)(x-2-3)=0,
解得:x1=2,x2=5;
(3)方程变形得:x2-2x=
,
配方得:x2-2x+1=
,即(x-1)2=
,
开方得:x-1=±
,
解得:x1=1+
,x2=1-
.
解得:x1=5,x2=-4;
(2)方程变形得:(x-2)2-3(x-2)=0,
分解因式得:(x-2)(x-2-3)=0,
解得:x1=2,x2=5;
(3)方程变形得:x2-2x=
| 9 |
| 2 |
配方得:x2-2x+1=
| 11 |
| 2 |
| 11 |
| 2 |
开方得:x-1=±
| ||
| 2 |
解得:x1=1+
| ||
| 2 |
| ||
| 2 |
点评:此题考查了解一元二次方程-分解因式法,配方法,熟练掌握因式分解法是解本题的关键.

练习册系列答案
相关题目
 如图所示,已知在△ABC中,AD垂直BC于D,CE垂直AB于E,连接DE,证明:△ABD∽△CBE,△BDE∽△BAC.
如图所示,已知在△ABC中,AD垂直BC于D,CE垂直AB于E,连接DE,证明:△ABD∽△CBE,△BDE∽△BAC.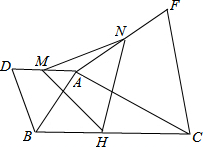 在△ABC中,以△ABC两侧作等边△ABD和等边△ACF,取AD和AF的中点M,N,再取BC的中点H,连接MN,MH,NH.推断并证明△MNH是什么三角形?
在△ABC中,以△ABC两侧作等边△ABD和等边△ACF,取AD和AF的中点M,N,再取BC的中点H,连接MN,MH,NH.推断并证明△MNH是什么三角形? 如图,已知AE=CF,∠AFD=∠CEB,需要添加一个条件使△ADF≌△CBE,这个条件可以为
如图,已知AE=CF,∠AFD=∠CEB,需要添加一个条件使△ADF≌△CBE,这个条件可以为