题目内容
6.某水果店总共筹备了5.1万资金计划购入一些时令水果销售(品种及价格如下表所示).现租用一辆载货量2.4吨的小货车进货(租金600元),要求将余下资金全部用于采购水果并使得所购水果装满货车.问应该怎样安排进货才能使水果店在销售完这批水果后获利最多?此时最大销售利润为多少元?| 水果名称 | 进货价(元/千克) | 销售价(元/千克) |
| 凤梨 | 10 | 19 |
| 芒果 | 26 | 36 |
| 荔枝 | 22 | 30 |
分析 设进货凤梨x千克,芒果y千克,荔枝z千克,根据筹备了5.1万资金计划购入一些时令水果销售(品种及价格如下表所示).现租用一辆载货量2.4吨的小货车进货(租金600元),得方程组$\left\{\begin{array}{l}10x+26y+22z=50400\\ x+y+z=24000\end{array}$,解得$\left\{\begin{array}{l}y=3x-600\\ z=3000-4x\end{array}$,再由$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{z≥0}\end{array}\right.$,求得x的取值范围,表示出利润的关系式,根据一次函数的性质,即可解答.
解答 解:设进货凤梨x千克,芒果y千克,荔枝z千克,51000-600=50400(元),
由题意可得:$\left\{\begin{array}{l}10x+26y+22z=50400\\ x+y+z=24000\end{array}$,
解得:$\left\{\begin{array}{l}y=3x-600\\ z=3000-4x\end{array}$,
由$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{z≥0}\end{array}\right.$,
得$\left\{\begin{array}{l}{x≥0}\\{3x-600≥0}\\{3000-4x≥0}\end{array}\right.$,
解得:200≤x≤750,
设销售利润为M,则M=9x+10y+8z=9x+10(3x-600)+8(3000-4x)=7x+18000,
∵k=7>0,
∴M随x的增大而增大,
当x=750时,M最大值=23250,
此时x=750,y=1650,z=0
即安排进货750千克凤梨和1650千克芒果可以使得销售利润最高为23250元.
点评 本题主要考查了一次函数的应用以及一元一次不等式组的应用和方程组的应用等知识,利用一次函数增减性得出函数最值是解题关键.

 考前必练系列答案
考前必练系列答案| A. | 4 | B. | 16 | C. | 14 | D. | 15 |
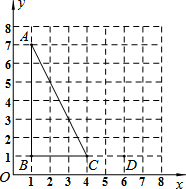 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )| A. | (4,0) | B. | (6,2) | C. | (6,3) | D. | (4,5) |
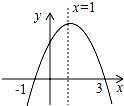 如图为二次函数y=ax2+bx+c的图象,给出下列说法:
如图为二次函数y=ax2+bx+c的图象,给出下列说法: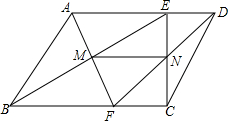 如图,在平行四边形ABCD中,E,F分别是AD,BC上的点,且AE=BF,BE交AF于M,CE交DF于N,求证:MN$\stackrel{∥}{=}$$\frac{1}{2}$AD.
如图,在平行四边形ABCD中,E,F分别是AD,BC上的点,且AE=BF,BE交AF于M,CE交DF于N,求证:MN$\stackrel{∥}{=}$$\frac{1}{2}$AD.