题目内容
9.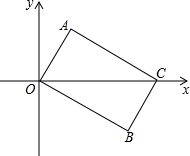 如图,己知平面直角坐标系中两点A(1,2)和C(5,0),且OA∥BC,AC∥OB,AC∥OB.
如图,己知平面直角坐标系中两点A(1,2)和C(5,0),且OA∥BC,AC∥OB,AC∥OB.(1)求证:四边形OBCA为矩形;
(2)直接写出B点坐标.
分析 (1)由已知条件证出四边形OBCA是平行四边形,作AM⊥OC于M,由勾股定理求出OA、AC,由勾股定理的逆定理证出∠OAC=90°,即可得出四边形OBCA是矩形;
(2)作BN⊥OC于N,由矩形的性质得出OA∥BC,OA=BC,证出∠AOC=∠BCO,由AAS证明△BCN≌△AOM,得出BN=AM=2,CN=OM=1,求出ON=OC-CN=4,即可得出点B坐标.
解答 (1)证明: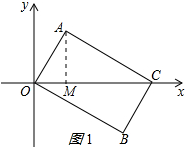 ∵OA∥BC,AC∥OB,
∵OA∥BC,AC∥OB,
∴四边形OBCA是平行四边形,
作AM⊥OC于M,如图1所示:
∵A(1,2),C(5,0),
∴OM=1,AM=2,OC=5,
∴CM=OC=OM=4,
∴OA=$\sqrt{O{M}^{2}+A{M}^{2}}$=$\sqrt{5}$,AC=$\sqrt{A{M}^{2}+C{M}^{2}}$=2$\sqrt{5}$,
∵OA2+AC2=25=OC2,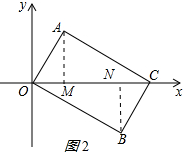
∴△AOC是直角三角形,∠OAC=90°,
∴四边形OBCA是矩形;
(2)解:作BN⊥OC于N,如图2所示:
则∠BNC=∠AMO=90°,
∵四边形OBCA是矩形,
∴OA∥BC,OA=BC,
∴∠AOC=∠BCO,
在△BCN和△AOM中,$\left\{\begin{array}{l}{∠BNC=∠AMO}&{\;}\\{∠AOC=∠BCO}&{\;}\\{BC=AO}&{\;}\end{array}\right.$,
∴△BCN≌△AOM(AAS),
∴BN=AM=2,CN=OM=1,
∴ON=OC-CN=4,
∴点B坐标为(4,-2).
点评 本题考查了平行四边形的判定、矩形的判定与性质、坐标与图形性质、勾股定理以及勾股定理的逆定理、全等三角形的判定与性质;证明三角形是直角三角形和三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.将点A(-4,-2)向右平移5的单位长度得到点B,则点B的所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.在平行四边形ABCD中,∠A:∠B:∠C=2:1:2,则∠D=( )
| A. | 60° | B. | 72° | C. | 108° | D. | 120° |
 如图,已知三角形ABC及三角形ABC外一点D,平移三角形ABC,使点A移动到点D,并保留画图痕迹.
如图,已知三角形ABC及三角形ABC外一点D,平移三角形ABC,使点A移动到点D,并保留画图痕迹.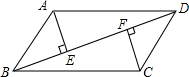 如图,BD是?ABCD的一条对角线,AE⊥BD,CF⊥BD,试猜想AE和CF的数量关系,并对你的猜想进行证明.
如图,BD是?ABCD的一条对角线,AE⊥BD,CF⊥BD,试猜想AE和CF的数量关系,并对你的猜想进行证明.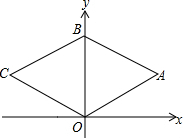 如图,菱形OABC顶点O是坐标原点,顶点B(0,6),OA=5.
如图,菱形OABC顶点O是坐标原点,顶点B(0,6),OA=5.