题目内容
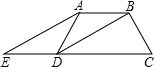 如图,在等腰梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.若∠E=30°,EC=12,求梯形ABCD的面积.
如图,在等腰梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.若∠E=30°,EC=12,求梯形ABCD的面积.考点:等腰梯形的性质
专题:
分析:根据两直线平行,同位角相等可得∠BDC=∠E=30°,再根据角平分线的定义可得∠ADC=2∠BDC,然后求出∠C=60°,∠CBD=90°,再求出AB=AD,判断出四边形AEDB是平行四边形,根据平行四边形的对边相等可得AB=DE,再根据EC的长度求出CD,然后解直角三角形求出CD边上的高,再根据梯形的面积公式列式计算即可得解.
解答:解:∵AE∥BD,
∴∠BDC=∠E=30°,
∵DB平分∠ADC,
∴∠ADC=2∠BDC=2×30°=60°,
在等腰梯形ABCD中,∠C=∠ADC=60°,
∴∠CBD=90°,
∴CD=2BC,
∵DB平分∠ADC,
∴∠ADB=∠CDB,
∵AB∥CD,
∴∠ABD=∠CDB,
∴∠ADB=∠ABD,
∴AB=AD,
∵AB∥DC,AE∥BD,
∴四边形AEDB是平行四边形,
∴AB=DE,
∴AB=DE=AD=BC,
∵EC=12,
∴DE+BC=DE+2DE=3DE=12,
解得DE=4,
BC=2DE=2×4=8,
点B到CD的距离为=BC×
=4×
=2
,
所以,梯形ABCD的面积=
×(4+8)×2
=12
.
∴∠BDC=∠E=30°,
∵DB平分∠ADC,
∴∠ADC=2∠BDC=2×30°=60°,
在等腰梯形ABCD中,∠C=∠ADC=60°,
∴∠CBD=90°,
∴CD=2BC,
∵DB平分∠ADC,
∴∠ADB=∠CDB,
∵AB∥CD,
∴∠ABD=∠CDB,
∴∠ADB=∠ABD,
∴AB=AD,
∵AB∥DC,AE∥BD,
∴四边形AEDB是平行四边形,
∴AB=DE,
∴AB=DE=AD=BC,
∵EC=12,
∴DE+BC=DE+2DE=3DE=12,
解得DE=4,
BC=2DE=2×4=8,
点B到CD的距离为=BC×
| ||
| 2 |
| ||
| 2 |
| 3 |
所以,梯形ABCD的面积=
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查了等腰梯形的性质,平行四边形的判定与性质,角平分线的定义,等腰三角形的判定,解直角三角形,关键在于求出ED、DC的长度.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
下列说法正确的是( )
| A、“明天降雨的概率是50%”表示明天有半天都在降雨 | ||||||||
| B、数据4,4,5,5,0的中位数和众数都是5 | ||||||||
| C、要了解一批钢化玻璃的最少允许碎片数,应采用普查的方式 | ||||||||
D、若甲、乙两组数中各有20个数据,平均数
|
下列命题中,正确的是( )
| A、过弦的中点的直线平分弦所对的弧 |
| B、过弦的中点的直线必经过圆心 |
| C、弦所对的两条弧的中点的连线垂直平分弦,且过圆心 |
| D、弦的垂线平分弦所对的弧 |
 如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点,函数y=ax2+bx+4过A,B,C三点且AB=6.
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点,函数y=ax2+bx+4过A,B,C三点且AB=6. 如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.