题目内容
19. 如图,抛物线y=ax2+bx+c交x轴于(-1,0),(2,0),则下列结论:①ac>0;②a+b=0;③当x$<\frac{1}{4}$时,y随x的增大而增大;④a-b+c<0.其中正确的个数有( )
如图,抛物线y=ax2+bx+c交x轴于(-1,0),(2,0),则下列结论:①ac>0;②a+b=0;③当x$<\frac{1}{4}$时,y随x的增大而增大;④a-b+c<0.其中正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 由图可知a<0,c>0,则ac<0,由抛物线与x轴坐标为(-1,0)和(2,0)可得当x=-1时,y=a-b+c=0,抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{1}{2}$,则有a+b=0,当x<$\frac{1}{2}$时,y随x的增大而增大.
解答 解:由图可知:a<0,c>0,则ac<0,故①错误;
抛物线与x轴坐标为(-1,0)和(2,0),
当x=-1时,y=0,则有a-b+c=0,故④错误;
抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{-1+2}{2}$=$\frac{1}{2}$,则有a+b=0,故②正确;
当x<$\frac{1}{2}$时,y随x的增大而增大,故③正确;
综上所述:正确的有2个.
故选C.
点评 本题主要考查了二次函数图象与系数的关系,二次函数与x轴的交点、二次函数的性质等知识,从图中读取有用的信息是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD放大为原来的2倍后得到线段AB,则端点B的坐标为( )
如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD放大为原来的2倍后得到线段AB,则端点B的坐标为( )
 如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD放大为原来的2倍后得到线段AB,则端点B的坐标为( )
如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD放大为原来的2倍后得到线段AB,则端点B的坐标为( )| A. | (6,6) | B. | (6,8) | C. | (8,6) | D. | (8,2) |
11.3.14-π的相反数为( )
| A. | 0 | B. | 3.14-π | C. | π-3.14 | D. | 0.14 |
 如图所示的圆柱体,它的底面半径为2cm,高为6cm.
如图所示的圆柱体,它的底面半径为2cm,高为6cm. 如图,在△ABC中,AB=AC=10cm,EF是边AB的垂直平分线,且△AEC的周长为24cm,则BC的长=14cm.
如图,在△ABC中,AB=AC=10cm,EF是边AB的垂直平分线,且△AEC的周长为24cm,则BC的长=14cm.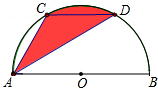 如图,已知AB为半圆O的直径,弦CD=8厘米,CD∥AB,∠CAD=30°,则图中阴影部分的面积等于$\frac{32π}{3}$平方厘米.
如图,已知AB为半圆O的直径,弦CD=8厘米,CD∥AB,∠CAD=30°,则图中阴影部分的面积等于$\frac{32π}{3}$平方厘米.