题目内容
某商店决定购进A,B两种纪念品,若购进A种纪念品10件,B种纪念品5件,需要1200元;若购进A种纪念品4件,B种纪念品3件,需要640元.
(1)购进A,B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量多于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
(1)购进A,B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量多于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
考点:一次函数的应用,二元一次方程组的应用,一元一次不等式组的应用
专题:
分析:(1)利用基本等量关系式:A种纪念品10要钱数+B种纪念品5钱数=1200元,A种念品4需要钱数+B种纪念品3需要钱数=640元;
(2)利用基本不等关系式:种纪念品需要的钱数+B种纪念品需要的钱数≤10000;购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍;
(3)计算出各种方案的利润,比较即可.
(2)利用基本不等关系式:种纪念品需要的钱数+B种纪念品需要的钱数≤10000;购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍;
(3)计算出各种方案的利润,比较即可.
解答:解:(1)设A纪念品每件需x元,B种纪念品每件需y元.
解得:
答:A纪念品每件需40元,B种纪念品每件需160元;
(2)设购买A种纪念品a件,B种纪念品b件.
解得
≤b≤25,
b=21、22、23、24、25,
a=250-4b,
则对应a=166、162、158、154、150
答:商店共有5种进货方案:进A种纪念品166件,B种纪念品21件;或A种纪念品162件,B种纪念品22件;或A种纪念品158件,B种纪念品23件;或A种纪念品154件,B种纪念品24件;或A种纪念品150件,B种纪念品25件;
(3)方案1利润为:166×20+21×30=3950(元);
方案2利润为:162×20+22×30=3900(元);
方案3利润为:158×20+23×30=3850(元);
方案4利润为:154×20+24×30=3800(元);
方案5利润为:150×20+25×30=3750(元);
故A种纪念品166件,B种纪念品21件利润较大为3950元.
|
解得:
|
答:A纪念品每件需40元,B种纪念品每件需160元;
(2)设购买A种纪念品a件,B种纪念品b件.
|
解得
| 125 |
| 6 |
b=21、22、23、24、25,
a=250-4b,
则对应a=166、162、158、154、150
答:商店共有5种进货方案:进A种纪念品166件,B种纪念品21件;或A种纪念品162件,B种纪念品22件;或A种纪念品158件,B种纪念品23件;或A种纪念品154件,B种纪念品24件;或A种纪念品150件,B种纪念品25件;
(3)方案1利润为:166×20+21×30=3950(元);
方案2利润为:162×20+22×30=3900(元);
方案3利润为:158×20+23×30=3850(元);
方案4利润为:154×20+24×30=3800(元);
方案5利润为:150×20+25×30=3750(元);
故A种纪念品166件,B种纪念品21件利润较大为3950元.
点评:此题主要考查了二元一次方程组的应用以及一元一次方程的应用,找到相应的关系式是解决问题的关键,注意第二问应求得整数解.

练习册系列答案
相关题目
两条直线相交有一个交点,三条直线相交最多有三个交点,n条直线相交最多有( )个交点.
| A、n | ||
| B、n(n-1) | ||
C、
| ||
D、
|
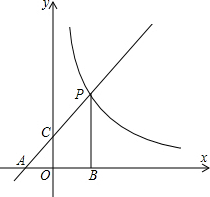 如图,直线y=
如图,直线y=
 已知一次函数y=kx+b(k≠0)的图象经过点(1,1)和点(0,-1).
已知一次函数y=kx+b(k≠0)的图象经过点(1,1)和点(0,-1). 已知:如图,△ABC中,∠B的平分线和△ABC的外角平分线交于点D,∠A=90°.求∠D的度数.
已知:如图,△ABC中,∠B的平分线和△ABC的外角平分线交于点D,∠A=90°.求∠D的度数. 如图,在菱形ABCD中,∠B=60°,AB=4,点E在BC上,BE=3EC,点F在DE上,满足:∠AFC=120°,EF>EC,则DF=
如图,在菱形ABCD中,∠B=60°,AB=4,点E在BC上,BE=3EC,点F在DE上,满足:∠AFC=120°,EF>EC,则DF=