题目内容
2.已知△ABC三边长分别为3,4,5,与和它相似的△DEF最小边的长为9,则△DEF的周长为36,面积是54.分析 由△ABC的三边长分别为3,4,5,与和它相似的△DEF最小边的长为9,即可求得△AC的周长以及相似比,又由相似三角形的周长的比等于相似比,可求得△DEF的周长.利用勾股定理逆定理判定△ABC是直角三角形,然后求出△ABC的面积,再根据相似三角形面积的比等于相似比的平方列式进行计算即可得△DEF的面积.
解答 解:∵△ABC的三边长分别为3,4,5,
∴△ABC的周长为:3+4+5=12,
∵与和它相似的△DEF最小边的长为9,
∴△DEF的周长:△ABC的周长=9:3=3:1,
∴△DEF的周长为:3×12=36;
∵32+42=25=52,
∴△ABC是直角三角形,
∴△ABC的面积=$\frac{1}{2}$×3×4=6,
∵△DEF与△ABC的相似比=9:3=3:1,
∴△DEF与△ABC的面积比=(3:1)2=9:1,
∴△DEF的面积=9×6=54.
故答案为:36,54.
点评 本题考查了相似三角形的性质,勾股定理逆定理的应用,熟记相似三角形周长的比等于相似比,面积的比等于相似比的平方是解题的关键.

练习册系列答案
相关题目
12.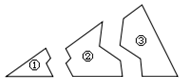 如图,小宇把一块三角形的玻璃打破成了三块,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是带( )去配.
如图,小宇把一块三角形的玻璃打破成了三块,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是带( )去配.
 如图,小宇把一块三角形的玻璃打破成了三块,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是带( )去配.
如图,小宇把一块三角形的玻璃打破成了三块,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是带( )去配.| A. | 第①块 | B. | 第②块 | C. | 第③块 | D. | 第①和②块 |
12.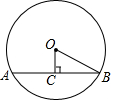 如图,在⊙O中,OC⊥AB于点C,AB=4,OC=1,则⊙O半径的长是( )
如图,在⊙O中,OC⊥AB于点C,AB=4,OC=1,则⊙O半径的长是( )
 如图,在⊙O中,OC⊥AB于点C,AB=4,OC=1,则⊙O半径的长是( )
如图,在⊙O中,OC⊥AB于点C,AB=4,OC=1,则⊙O半径的长是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{15}$ | D. | $\sqrt{17}$ |