题目内容
5. 如图,AB是⊙O的直径,弦BC=8,∠BOC=60°,OE⊥AC,垂足为E.
如图,AB是⊙O的直径,弦BC=8,∠BOC=60°,OE⊥AC,垂足为E.(1)求OE的长;
(2)求劣弧AC的长.
分析 (1)由垂径定理知,由E是AC的中点,点O是AB的中点,则OB是△ABC的BC边对的中位线,所以OE=$\frac{1}{2}$BC;
(2)由圆周角定理得∠A=$\frac{1}{2}$∠BOC=30°,根据平角的意义求得∠AOC的度数,再利用弧长公式求得弧AC的长.
解答 解:(1)∵OE⊥AC,垂足为E,AE=EC,
∵AO=B0,
∴OE=$\frac{1}{2}$BC=4;
(2)∵∠A与∠BOC是同弧所对的圆周角与圆心角,
∴∠A=$\frac{1}{2}$∠BOC=30°,
在Rt△AOE中,sinA=$\frac{OE}{OA}$,即OA=$\frac{OE}{sin∠A}$=$\frac{4}{sin30°}$=8,
∵∠AOC=180°-60°=120°,
∴弧AC的长=$\frac{120π×{8}^{2}}{360}$=$\frac{64}{3}$π.
点评 本题利用了垂径定理,三角形中位线的性质,圆周角定理,正弦的概念,弧长公式求解.

练习册系列答案
相关题目
15.-$\sqrt{5}$的相反数是( )
| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
14.为美化市容,某广场要在人行甬道上用10×20的灰、白两色的广场砖铺设图案,设计人员画出的一些备选图案如图所示.(1)由于选用图案的不同,使用的两种广场砖的块数也不同,请你认真观察思考后,填写下表:
(2)求出白砖数恰好比灰砖数少1时的n值;
(3)是否存在白砖数恰好等于灰砖数的n值,说明你的理由;
(4)若每块白砖售价为2元,每块灰砖售价为3元,每块砖的施工费用为0.5元,铺设一个图案的费用为y元,请求出y与n的函数关系式(不要求写自变量n的取值范围).

| 图案序号n | 1 | 2 | 3 | … | n |
| 使用的灰砖块数 | 1 | 4 | … | ||
| 使用的白砖块数 | 8 | … |
(3)是否存在白砖数恰好等于灰砖数的n值,说明你的理由;
(4)若每块白砖售价为2元,每块灰砖售价为3元,每块砖的施工费用为0.5元,铺设一个图案的费用为y元,请求出y与n的函数关系式(不要求写自变量n的取值范围).

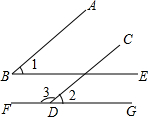 如图,已知AB∥CD,BE∥FG.
如图,已知AB∥CD,BE∥FG. 探索与证明:
探索与证明: 如图,有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来为HELLO.
如图,有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来为HELLO.
 如图,已知a∥b,将三角板的直角顶点放置在直线b上,若∠1=50°,则∠2的度数为40°.
如图,已知a∥b,将三角板的直角顶点放置在直线b上,若∠1=50°,则∠2的度数为40°.