题目内容
1.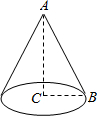 如图,△ABC中,∠ACB=90°,AC=4,BC=3,把△ABC绕AC边旋转一周(360°)得到一个圆锥体,那么这个圆锥体的侧面积为15π(结果可保留π)
如图,△ABC中,∠ACB=90°,AC=4,BC=3,把△ABC绕AC边旋转一周(360°)得到一个圆锥体,那么这个圆锥体的侧面积为15π(结果可保留π)
分析 先根据勾股定理计算出AB=5,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式求解.
解答 解:∵∠ACB=90°,AC=4,BC=3,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴这个圆锥体的侧面积=$\frac{1}{2}$•2π•3•5=15π.
故答案为15π.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
12.若a-b=1,ab=-2,则(a+1)(b-1)=( )
| A. | -4 | B. | 4 | C. | -3 | D. | 3 |
6.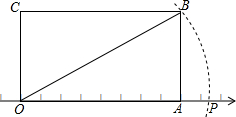 如图,矩形OABC的顶点O是数轴的原点,长边OA在数轴上,点A所表示的数为8,OC的长为$\sqrt{24}$,以O为圆心OB为半径的圆弧与数轴交于P点,则P点表示的数是( )
如图,矩形OABC的顶点O是数轴的原点,长边OA在数轴上,点A所表示的数为8,OC的长为$\sqrt{24}$,以O为圆心OB为半径的圆弧与数轴交于P点,则P点表示的数是( )
 如图,矩形OABC的顶点O是数轴的原点,长边OA在数轴上,点A所表示的数为8,OC的长为$\sqrt{24}$,以O为圆心OB为半径的圆弧与数轴交于P点,则P点表示的数是( )
如图,矩形OABC的顶点O是数轴的原点,长边OA在数轴上,点A所表示的数为8,OC的长为$\sqrt{24}$,以O为圆心OB为半径的圆弧与数轴交于P点,则P点表示的数是( )| A. | 2$\sqrt{6}$ | B. | 9.5 | C. | 2$\sqrt{22}$ | D. | 4$\sqrt{11}$ |
11.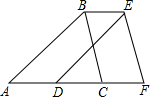 如图,将△ABC沿AC方向平移1cm得到△DEF,若△ABC的周长为10cm.则四边形ABEF的周长为( )
如图,将△ABC沿AC方向平移1cm得到△DEF,若△ABC的周长为10cm.则四边形ABEF的周长为( )
 如图,将△ABC沿AC方向平移1cm得到△DEF,若△ABC的周长为10cm.则四边形ABEF的周长为( )
如图,将△ABC沿AC方向平移1cm得到△DEF,若△ABC的周长为10cm.则四边形ABEF的周长为( )| A. | 10cm | B. | 11cm | C. | 12cm | D. | 14cm |
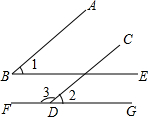 如图,已知AB∥CD,BE∥FG.
如图,已知AB∥CD,BE∥FG.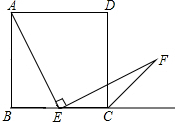 探索与证明:
探索与证明: