题目内容
10.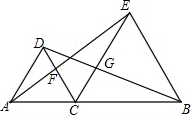 已知:C是AB上的一点,以AC为边作等边△ACD,以BC为边向AD所在的一侧作等边△BCE,AE、CD相交于F,BD、CE相交于G.求证:CF=CG.
已知:C是AB上的一点,以AC为边作等边△ACD,以BC为边向AD所在的一侧作等边△BCE,AE、CD相交于F,BD、CE相交于G.求证:CF=CG.
分析 先根据SAS即可证明△ACE≌△BCD;再证明△DCG≌△ACF,从而得出CG=CF.
解答 解:∵△DAC是等边三角形,
∴AC=DC,∠ACD=60°,
∵△BCE为等边三角形,
∴CE=CB,∠ECB=60°,
∴∠ACD=∠ECB=60°,
∴∠ACD+∠DCE=∠ECB+∠DCE,
即∠ACE=∠BCD,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AD=DC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD(SAS);
∴∠CAE=∠CDB,
∵∠ACD=∠ECB=60°
∴∠DCG=60°
∴∠ACD=∠DCG,
在△ACF和△DCG中,
$\left\{\begin{array}{l}{∠CAF=∠CDG}\\{AC=DC}\\{∠ACD=∠DCG}\end{array}\right.$,
∴△ACF≌△DCG(SAS),
∴CG=CF.
点评 本题考查了全等三角形的判定和性质以及等边三角形的判定和性质,解决本题的关键是证明三角形全等.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
1.巴黎与北京的时差为-7小时(正数表示同一时刻比北京早的时数),如果北京时间是10月2日14时,那么巴黎时间是( )
| A. | 10月2日21时 | B. | 10月2日7时 | C. | 10月2日5时 | D. | 10月1日7时 |
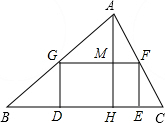 如图,在△ABC中,矩形DEFG的一边DE在BC上,另外两个顶点G,F分别在AB,AC上,高AH交GF于M,且BC=8,AH=5,矩形DEFG的周长为12.求△AGF的面积.
如图,在△ABC中,矩形DEFG的一边DE在BC上,另外两个顶点G,F分别在AB,AC上,高AH交GF于M,且BC=8,AH=5,矩形DEFG的周长为12.求△AGF的面积.
 如图,已知牧马营地C和D,某一天,牧马人从营地C赶着马群,先带到草地吃草,再到河边饮水,然后回到营地D,请你替牧马人设计出最短路线.
如图,已知牧马营地C和D,某一天,牧马人从营地C赶着马群,先带到草地吃草,再到河边饮水,然后回到营地D,请你替牧马人设计出最短路线. .
.