题目内容
9.小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数(单位:公里)如下:| 时刻 | 9:00 | 9:48 | 11:00 |
| 里程碑上的数 | 是一个两位数,它的两个数字之和为6 | 也是一个两位数,十位与个位数字与9:00时所看到的正好互换了 | 是一个三位数,比9:00时看到的两位数的数字中间多了个0 |
(1)小明9:00时看到的两位数为10x+y;
(2)小明9:48时看到的两位数为10y+x;11:00时看到的两位数为100x+y;
(3)请你列二元一次方程求小明在9:00时看到里程碑上的两位数.
分析 (1)、(2)根据一个两位数=十位数字×10+个位数字;
(3)表示出摩托车的速度,根据车速不变列方程组求解即可.
解答 解:(1)9:00时,两位数可表示为10x+y;
故答案为;10x+y.
(2)9:48时,两位数可表示为10y+x;11:00看到的数字可表示为:100x+y;
故答案为;10y+x;100x+y.
(3)根据题意得;$\left\{\begin{array}{l}{x+y=6}\\{\frac{100x+y-(10x+y)}{120}=\frac{10y+x-(10x+y)}{48}}\end{array}\right.$.
解得:$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.$
∴小明在9:00时看到里程碑上的两位数是15.
答:小明在9:00时看到里程碑上的两位数是15.
点评 本题主要考查的是二元一次方程组的应用,根据车速不变以及两个数字的和是6列出方程组是解题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
14.若点A(a+1,b-1)在第二象限,则点B(-a,b+2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
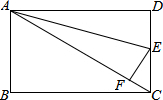 已知:如图,长方形ABCD中,AB=6,AD=8,沿直线AE把△ADE折叠,点O恰好落在AC上一点F处.
已知:如图,长方形ABCD中,AB=6,AD=8,沿直线AE把△ADE折叠,点O恰好落在AC上一点F处. 如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP=6.
如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP=6.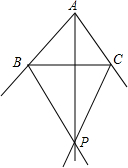 已知,如图所示,在△ABC中,PB,PC分别是△ABC的两个外角的平分线,求证:AP平分∠BAC.
已知,如图所示,在△ABC中,PB,PC分别是△ABC的两个外角的平分线,求证:AP平分∠BAC.