题目内容
12.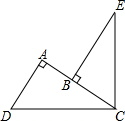 如图,∠DCE=90°,CD=CE,DA⊥AC,EB⊥AC,垂足分别为点A、B.
如图,∠DCE=90°,CD=CE,DA⊥AC,EB⊥AC,垂足分别为点A、B.试说明AD+AB=BE.
解:因为 DA⊥AC,EB⊥AC(已知),
所以∠A=∠EBC=90°(垂直的意义).
又因为∠A+∠D+∠ACD=180°(三角形的内角和等于180°),
得∠D+∠ACD=90°.
因为∠DCE=90° (已知),
得∠BCE+∠ACD=90°,
∴∴∠ECB=∠D,
在△ECB和△CDA中,$\left\{\begin{array}{l}{∠ECB=∠D}\\{∠EBC=∠A=90°}\\{CE=CD}\end{array}\right.$,
∴△ECB≌△CDA(AAS),
∴BC=AD,BE=AC,
∴AD+AB=AB+BC=AC=BE.(同角的余角相等).
(完成以下说理过程)
分析 利用同角的余角相等得到一对角相等,再由一对直角相等,CD=CE,利用AAS得到三角形ECB与三角形CDA全等,利用全等三角形对应边相等得到BC=AD,BE=AC,由AB+BC=AC=BE,等量代换即可得证.
解答 解:因为 AD⊥AC,BE⊥AC(已知),
所以∠A=∠EBC=90°(垂直的意义).
又因为∠A+∠D+∠ACD=180°(三角形的内角和等于180°)
得∠D+∠ACD=90°.
因为∠DCE=90° (已知),
得∠BCE+∠ACD=90°,
∴∠ECB=∠D,
在△ECB和△CDA中,$\left\{\begin{array}{l}{∠ECB=∠D}\\{∠EBC=∠A=90°}\\{CE=CD}\end{array}\right.$,
∴△ECB≌△CDA(AAS),
∴BC=AD,BE=AC,
∴AD+AB=AB+BC=AC=BE.
故答案为:三角形的内角和等于180°,∴∠ECB=∠D,
在△ECB和△CDA中,$\left\{\begin{array}{l}{∠ECB=∠D}\\{∠EBC=∠A=90°}\\{CE=CD}\end{array}\right.$,
∴△ECB≌△CDA(AAS),
∴BC=AD,BE=AC,
∴AD+AB=AB+BC=AC=BE.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
4.已知点M(3,-2),N(-3,-2),则直线MN与x轴、y轴的位置关系分别为( )
| A. | 相交,相交 | B. | 平行,平行 | C. | 垂直相交,平行 | D. | 平行,垂直相交 |
 如图,线段OB与射线OA有一公共端点O,在所给图中,用直尺和圆规按所给的语句作图.(注:按题目要求作图,保留痕迹,不必写作法)
如图,线段OB与射线OA有一公共端点O,在所给图中,用直尺和圆规按所给的语句作图.(注:按题目要求作图,保留痕迹,不必写作法)