题目内容
20.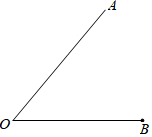 如图,线段OB与射线OA有一公共端点O,在所给图中,用直尺和圆规按所给的语句作图.(注:按题目要求作图,保留痕迹,不必写作法)
如图,线段OB与射线OA有一公共端点O,在所给图中,用直尺和圆规按所给的语句作图.(注:按题目要求作图,保留痕迹,不必写作法)(1)在射线OA上截取线段OC,使OC=OB;
(2)联结BC,作线段CB的中点M;
(3)作∠AOB的平分线OD;
(4)以OB为一边在∠AOB的外部作∠BOE,使∠BOE=∠AOB.如果∠AOB=50°,那么∠DOE=75度.
分析 (1)利用基本作图(作一条线段等于已知线段)画出OC;
(2)作BC的垂直平分线可得到BC的中点;
(3)利用等腰三角形的性质,连接OM即可;
(4)先利用角平分线的定义得到∠DOB=$\frac{1}{2}$∠AOB=25°,然后计算∠DOB+∠BOE即可.
解答 解:(1)如图,OC为所作;
(2)如图,点M为所作;
(3)如图,OD为所作;
(4)∵M点为BC的中点,OC=OB,
∴OM平分∠AOB,
∴∠DOB=$\frac{1}{2}$∠AOB=25°,
∴∠DOE=∠DOB+∠BOE=25°+50°=75°.
故答案为75.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了等腰三角形的性质.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图所示,直线AB、CD、EF相交于点O,且AB⊥CD,OG平分∠AOE,若∠DOF=50°,求∠AOG的度数.
如图所示,直线AB、CD、EF相交于点O,且AB⊥CD,OG平分∠AOE,若∠DOF=50°,求∠AOG的度数.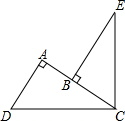 如图,∠DCE=90°,CD=CE,DA⊥AC,EB⊥AC,垂足分别为点A、B.
如图,∠DCE=90°,CD=CE,DA⊥AC,EB⊥AC,垂足分别为点A、B.