题目内容
如图，BC与⊙O相切于点C，BO的延长线交⊙O于点A，连结AC，若∠ACB=120°，则∠A的度数等于（ ）| A、30° | B、40° |
| C、50° | D、60° |
考点：切线的性质
专题：
分析：如图，连接OC．根据切线的性质知∠OCB=90°，则易求∠A=∠ACO=120°-90°=30°．
解答：
解：如图，连接OC．
∵BC与⊙O相切于点C，
∴OC⊥BC，即∠OCB=90°．
∵A=OC，
∴∠A=∠ACO=∠ACB-∠OCB=120°-90°=30°．
故选A．
解：如图，连接OC．∵BC与⊙O相切于点C，
∴OC⊥BC，即∠OCB=90°．
∵A=OC，
∴∠A=∠ACO=∠ACB-∠OCB=120°-90°=30°．
故选A．
点评：本题考查了圆的切线性质．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
相关题目
如图，以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，AB=12，AO=8，则OC长为（ ）| A、5 | ||
| B、4 | ||
C、2
| ||
D、2
|
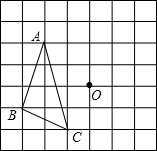如图，正方形网格中每个小正方形的边长均为l，△ABC的三个顶点都在格点上，现将△ABC绕着格点O顺时针旋转90°
如图，在平面直角坐标系中，作出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标．