题目内容
5.对于任意正整数n,整式(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的倍数,试说明理由.分析 利用平方差公式对整式(3n+1)(3n-1)-(3-n)(3+n)进行化简,然后化成10乘以一个整式的形式即可.
解答 解:(3n+1)(3n-1)-(3-n)(3+n)
=9n2-1-(9-n2)
=9n2-1-9+n2
=10n2-10
=10(n2-1).
则整式(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的倍数.
点评 本题考查了整数的化简,正确理解平方差公式是解决本题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
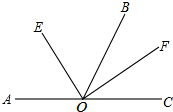 如图,AC为一条直线,O是AC上一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC.
如图,AC为一条直线,O是AC上一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC. 已知等边三角形ABC的边长为2,将这个三角形放置在如图所示的直角坐标系中,且B,C两点的坐标分别为(-1,0),(1,0)
已知等边三角形ABC的边长为2,将这个三角形放置在如图所示的直角坐标系中,且B,C两点的坐标分别为(-1,0),(1,0) 如图所示的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,整架身,使点A恰好在重锤线上,试问:此时BC是否正好处于水平位置?为什么?
如图所示的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,整架身,使点A恰好在重锤线上,试问:此时BC是否正好处于水平位置?为什么?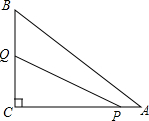 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,当点P停止运动时,点Q也随之停止,点P,Q同时出发,设点P的运动时间为t(秒).
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,当点P停止运动时,点Q也随之停止,点P,Q同时出发,设点P的运动时间为t(秒).