题目内容
3. 如图,一游人由山脚A沿坡角为30°的山坡AB行走600m,到达一个景点B,再由B沿山坡BC行走200m到达山顶C,若在山顶C处观测到景点B的俯角为45°,则山高CD=300+100$\sqrt{2}$m(结果用根号表示).
如图,一游人由山脚A沿坡角为30°的山坡AB行走600m,到达一个景点B,再由B沿山坡BC行走200m到达山顶C,若在山顶C处观测到景点B的俯角为45°,则山高CD=300+100$\sqrt{2}$m(结果用根号表示).
分析 过B作BF⊥AD于F,BE⊥CD于E,根据俯角的定义得到∠BCE=45°,再根据等腰直角三角形的性质得到CE=$\frac{\sqrt{2}}{2}$BC=100$\sqrt{2}$m;又∠A=30°,AB=600m,根据含30度的直角三角形三边的关系得到BF=$\frac{1}{2}$AB=300m,最后由CD=CE+ED=CE+BF得到结果.
解答 解:过B作BF⊥AD于F,BE⊥CD于E,如图:
∵在山顶C处测得景点B的俯角为45°,
∴∠BCE=45°,
∴△BCE为等腰直角三角形,
∵BC=200m,
∴CE=$\frac{\sqrt{2}}{2}$BC=100$\sqrt{2}$m;
∵∠A=30°,AB=600m,
∴BF=$\frac{1}{2}$AB=300m,
∴CD=CE+ED=CE+BF=(300+100$\sqrt{2}$)m.
故答案为:300+100$\sqrt{2}$m.
点评 本题考查了解直角三角形的应用-仰角俯角:向下看,视线与水平线的夹角叫俯角;坡角为坡面与水平面的夹角.也考查了等腰直角三角形和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
11. 如图,直角三角形三边向形外作了三个正方形,其中数字表示该正方形的面积,那么正方形A的面积是( )
如图,直角三角形三边向形外作了三个正方形,其中数字表示该正方形的面积,那么正方形A的面积是( )
 如图,直角三角形三边向形外作了三个正方形,其中数字表示该正方形的面积,那么正方形A的面积是( )
如图,直角三角形三边向形外作了三个正方形,其中数字表示该正方形的面积,那么正方形A的面积是( )| A. | 360 | B. | 164 | C. | 400 | D. | 60 |
18.某市体育协会对2400名年满15岁的男生的身高进行了测量,结果身高(单位:m)在1.68-1.70这一小组的频率为0.25,则该组的人数为( )
| A. | 600人 | B. | 250人 | C. | 60人 | D. | 25人 |
15.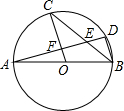 如图,AB为⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.若∠CBD=36°,则下列结论中不正确的是( )
如图,AB为⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.若∠CBD=36°,则下列结论中不正确的是( )
 如图,AB为⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.若∠CBD=36°,则下列结论中不正确的是( )
如图,AB为⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.若∠CBD=36°,则下列结论中不正确的是( )| A. | ∠AOC=72° | B. | ∠AEC=72° | C. | AF=DF | D. | BD=20F |

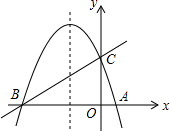 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B. 如图,△ABC中,AB=AC,D点在BC上,∠BAD=30°,且∠ADC=60°.请完整说明为何AD=BD与CD=2BD的理由.
如图,△ABC中,AB=AC,D点在BC上,∠BAD=30°,且∠ADC=60°.请完整说明为何AD=BD与CD=2BD的理由.