题目内容
4.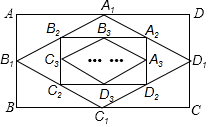 如图,顺次连接矩形ABCD四边的中点得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得到四边形A3B3C3D3,…,已知AB=6,BC=8,按此方法得到的四边形A5B5C5D5的周长为5.
如图,顺次连接矩形ABCD四边的中点得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得到四边形A3B3C3D3,…,已知AB=6,BC=8,按此方法得到的四边形A5B5C5D5的周长为5.
分析 根据三角形中位线性质定理可得每一次去各边中点所形成新的四边形周长都为前一个的$\frac{1}{2}$;并且四边形是平行四边形,即可计算四边形A5B5C5D5的周长.
解答 解:由勾股定理得到AC=BD=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
根据中位线的性质易知,A5B5=$\frac{1}{2}$A3B3×$\frac{1}{2}$A1B1=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$AC=$\frac{1}{8}$×10=$\frac{5}{4}$;
B5C5=$\frac{1}{2}$B3C3×$\frac{1}{2}$B1C1=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$BD=$\frac{5}{4}$,
∴四边形A5B5C5D5的周长是2×($\frac{5}{4}$+$\frac{5}{4}$)=5.
故答案为:5.
点评 本题考查了中点四边形,需要掌握三角形的中位线性质定理:三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
12.若关于x的方程$\frac{a-2x}{x+2}$=1的解是负数,则a的取值范围是( )
| A. | a<2 | B. | a>2 | C. | a<2,且a≠-4 | D. | a>2,且a≠4 |
9.首都国际机场连续五年排名全球最繁忙机场第二位,该机场2012-2016年客流量统计结果如表:
根据统计表中提供的信息,预估首都国际机场2017年客流量约9823万人次,你的预估理由是由之前连续3年增长率预估2017年客流量的增长率约为4.5%.
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 客流量(万人次) | 8192 | 8371 | 8613 | 8994 | 9400 |
15.若x3•xmy2n=x9y8,则m+n等于( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
 在直角坐标中反比例函数y=$\frac{6}{x}$的图象如图所示.
在直角坐标中反比例函数y=$\frac{6}{x}$的图象如图所示.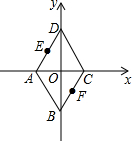 以菱形ABCD的对角线交点O为原点,对角线AC、BD所在直线为坐标轴,建立如图所示直角坐标系,AD的中点E的坐标为(-1,2),则BC的中点F的坐标为(1,-2).
以菱形ABCD的对角线交点O为原点,对角线AC、BD所在直线为坐标轴,建立如图所示直角坐标系,AD的中点E的坐标为(-1,2),则BC的中点F的坐标为(1,-2).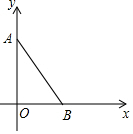 如图,平面直角坐标系xOy中,已知点A(0,3),点B($\sqrt{3}$,0),连接AB,若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
如图,平面直角坐标系xOy中,已知点A(0,3),点B($\sqrt{3}$,0),连接AB,若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.