Question

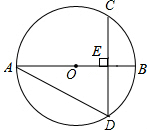如图，在⊙O中，弦CD垂直于直径AB于点E，若∠BAD=30°，且BE=2，则CD=

 

．

Answer 1

考点：垂径定理,解直角三角形

专题：计算题

分析：连结OD，设⊙O的半径为R，先根据圆周角定理得到∠BOD=2∠BAD=60°，再根据垂径定理由CD⊥AB得到DE=CE，在Rt△ODE中，OE=OB-BE=R-2，利用余弦的定义得cos∠EOD=cos60°=

OE

OD

，即

R-2

R

=

1

2

，解得R=4，则OE=2，DE=

3

OE=2

3

，所以CD=2DE=4

3

．

解答：解：连结OD，如图，设⊙O的半径为R，
∵∠BAD=30°，
∴∠BOD=2∠BAD=60°，
∵CD⊥AB，
∴DE=CE，
在Rt△ODE中，OE=OB-BE=R-2，OD=R，
∵cos∠EOD=cos60°=

OE

OD

，
∴

R-2

R

=

1

2

，解得R=4，
∴OE=4-2=2，
∴DE=

3

OE=2

3

，
∴CD=2DE=4

3

故答案为：4

3

．

点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了圆周角定理和解直角三角形．