题目内容
 如图,在数轴上,从原点A开始,以AB=1为边长画等边三角形,记为第一个等边三角形;以BC=2为边长画等边三角形,记为第二个等边三角形;以CD=4为边长画等边三角形,记为第三个等边三角形;以DE=8为边长画等边三角形,记为第四个等边三角形;…按此规律,继续画等边三角形,那么第五个等边三角形的面积是
如图,在数轴上,从原点A开始,以AB=1为边长画等边三角形,记为第一个等边三角形;以BC=2为边长画等边三角形,记为第二个等边三角形;以CD=4为边长画等边三角形,记为第三个等边三角形;以DE=8为边长画等边三角形,记为第四个等边三角形;…按此规律,继续画等边三角形,那么第五个等边三角形的面积是考点:规律型:图形的变化类,等边三角形的性质
专题:
分析:每一个等边三角形的边长分别为1、2、4、8、16、…2n-1,分别计算出每一个等边三角形的面积,找出规律,进一步利用规律得出答案即可.
解答:解:第一个边长为1等边三角形的面积为
×1×
=
,
第二个边长为2等边三角形的面积为
×2×
=
,
第三个边长为4等边三角形的面积为
×4×2
=4
,
第四个边长为8等边三角形的面积为
×8×4
=16
,
第五个边长为16等边三角形的面积为
×16×8
=64
,
…
第n个边长为2n-1等边三角形的面积为
×2n-1×2n-2
=22n-4
.
故答案为:64
,22n-4
.
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
第二个边长为2等边三角形的面积为
| 1 |
| 2 |
| 3 |
| 3 |
第三个边长为4等边三角形的面积为
| 1 |
| 2 |
| 3 |
| 3 |
第四个边长为8等边三角形的面积为
| 1 |
| 2 |
| 3 |
| 3 |
第五个边长为16等边三角形的面积为
| 1 |
| 2 |
| 3 |
| 3 |
…
第n个边长为2n-1等边三角形的面积为
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:64
| 3 |
| 3 |
点评:此题考查图形的变化规律,从简单情形入手,找出运算的规律解决问题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
四边形ABCD中,对角线AC=BD,点E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH是( )
| A、正方形 | B、矩形 |
| C、等腰梯形 | D、菱形 |

 如图,直线a∥b,直线c与直线a,b都相交,∠1=65°,则∠2=
如图,直线a∥b,直线c与直线a,b都相交,∠1=65°,则∠2= 如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:
如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件: 如图,在矩形ABCD中,
如图,在矩形ABCD中, 关于x的反比例函数y=
关于x的反比例函数y=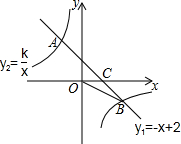 如图,一次函数y1=-x+2的图象与反比例函数y2=
如图,一次函数y1=-x+2的图象与反比例函数y2=