题目内容
1.计算:(1)3$\sqrt{2}+\sqrt{8}$;
(2)$\sqrt{\frac{2}{5}}×\sqrt{10}+\frac{\sqrt{32}}{\sqrt{8}}$;
(3)($\sqrt{5}+\sqrt{2}$)2;
(4)$\sqrt{12}-\sqrt{3}+\sqrt{\frac{1}{3}}$.
分析 (1)先把$\sqrt{8}$化为最简二次根式,然后合并即可;
(2)利用二次根式的乘除法则运算;
(3)利用完全平方公式计算;
(4)先把各二次根式化为最简二次根式,然后合并即可.
解答 解:(1)原式=3$\sqrt{2}$+2$\sqrt{2}$
=5$\sqrt{2}$;
(2)原式=$\sqrt{\frac{2}{5}×10}$+$\sqrt{\frac{32}{8}}$
=2+2
=4;
(3)原式=5+2$\sqrt{10}$+2
=7+2$\sqrt{10}$;
(4)原式=2$\sqrt{3}$-$\sqrt{3}$+$\frac{\sqrt{3}}{3}$
=$\frac{4\sqrt{3}}{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
12.下来各数中,比-1小的数是( )
| A. | 0 | B. | 1 | C. | -1 | D. | -$\sqrt{2}$ |
16. 如图,已知点P的坐标为(12,5),则点P到原点O的距离为( )
如图,已知点P的坐标为(12,5),则点P到原点O的距离为( )
 如图,已知点P的坐标为(12,5),则点P到原点O的距离为( )
如图,已知点P的坐标为(12,5),则点P到原点O的距离为( )| A. | 5 | B. | 12 | C. | 13 | D. | 17 |
13.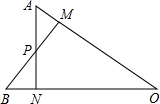 如图,AN⊥OB,BM⊥OA,垂足分别是N、M,BM与AN交于点P,若OM=ON,则下列结论不正确的是( )
如图,AN⊥OB,BM⊥OA,垂足分别是N、M,BM与AN交于点P,若OM=ON,则下列结论不正确的是( )
 如图,AN⊥OB,BM⊥OA,垂足分别是N、M,BM与AN交于点P,若OM=ON,则下列结论不正确的是( )
如图,AN⊥OB,BM⊥OA,垂足分别是N、M,BM与AN交于点P,若OM=ON,则下列结论不正确的是( )| A. | OA=OB | B. | AM=BN | ||
| C. | 点P在∠AOB的平分线上 | D. | AM=PM |
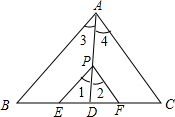 如图所示,已知△ABC中,PE∥AB交BC于E,PF∥AC交BC于F,P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
如图所示,已知△ABC中,PE∥AB交BC于E,PF∥AC交BC于F,P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.