题目内容
4.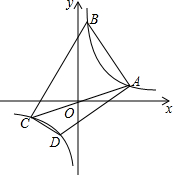 如图,在平面直角坐标中,四边形ABCD的四个顶点都在双曲线y=$\frac{1}{x}$上,其中,点A、B在第一象限,点C、D在第三象限,对角线AC经过原点O,求证:∠BAD=∠BCD.
如图,在平面直角坐标中,四边形ABCD的四个顶点都在双曲线y=$\frac{1}{x}$上,其中,点A、B在第一象限,点C、D在第三象限,对角线AC经过原点O,求证:∠BAD=∠BCD.
分析 延长BA交x轴于F,延长DC交x轴于M,过点B作BH⊥x轴于H,如图所示.设点A(a,$\frac{1}{a}$),点B(b,$\frac{1}{b}$),则点C(-a,-$\frac{1}{a}$).然后运用待定系数法求出直线AB的解析式,然后求出直线AB与x轴的交点F的坐标,然后根据三角函数的定义求得tan∠BFH=$\frac{1}{ab}$,同理可得tan∠BEH=$\frac{1}{ab}$,即可得到∠BFH=∠BEH,从而可得∠BFH=∠MEC,同理可得∠ANF=∠DMO,然后根据三角形外角的性质可得∠BAD=∠BCD.
解答 证明:延长BA交x轴于F,延长DC交x轴于M,过点B作BH⊥x轴于H,如图所示.
设点A(a,$\frac{1}{a}$),点B(b,$\frac{1}{b}$),则点C(-a,-$\frac{1}{a}$).
设直线AB的解析式为y=mx+n,
则有$\left\{\begin{array}{l}{\frac{1}{a}=am+n}\\{\frac{1}{b}=bm+n}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-\frac{1}{ab}}\\{n=\frac{a+b}{ab}}\end{array}\right.$,.
∴直线AB的解析式为y=-$\frac{1}{ab}$x+$\frac{a+b}{ab}$,
当y=0时,x=a+b,则F(a+b,0).
在Rt△BHF中,tan∠BFH=$\frac{BH}{HF}$=$\frac{\frac{1}{b}}{a+b-b}$=$\frac{1}{ab}$.
同理可得:tan∠BEH=$\frac{BH}{EH}$=$\frac{1}{ab}$,
∴tan∠BFH=tan∠BEH,
∴∠BFH=∠BEH.
∵∠MEC=∠BEH,
∴∠BFH=∠MEC.
同理可得:∠ANF=∠DMO.
∵∠BCD=∠MEC+∠DMO,∠BAD=∠BFH+∠ANF,
∴∠BAD=∠BCD.
点评 本题主要考查了反比例函数图象上点的坐标特征、用待定系数法求直线的解析式、求直线与x轴的交点坐标、三角函数的定义、三角形外角的性质等知识,证到直线BA、BC与x轴所成的锐角相等及直线DA、DC与x轴所成的锐角相等,是解决本题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 0 | B. | 1 | C. | -1 | D. | -$\sqrt{2}$ |
 如图,已知点P的坐标为(12,5),则点P到原点O的距离为( )
如图,已知点P的坐标为(12,5),则点P到原点O的距离为( )| A. | 5 | B. | 12 | C. | 13 | D. | 17 |
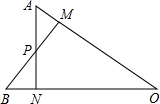 如图,AN⊥OB,BM⊥OA,垂足分别是N、M,BM与AN交于点P,若OM=ON,则下列结论不正确的是( )
如图,AN⊥OB,BM⊥OA,垂足分别是N、M,BM与AN交于点P,若OM=ON,则下列结论不正确的是( )| A. | OA=OB | B. | AM=BN | ||
| C. | 点P在∠AOB的平分线上 | D. | AM=PM |
 数a,b,c在数轴上的位置如图所示,化简|a-c|+|b-c|+|a+b|.
数a,b,c在数轴上的位置如图所示,化简|a-c|+|b-c|+|a+b|. △ABC和点S在平面直角坐标系中的位置如图所示.
△ABC和点S在平面直角坐标系中的位置如图所示.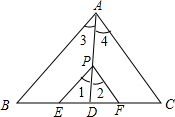 如图所示,已知△ABC中,PE∥AB交BC于E,PF∥AC交BC于F,P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
如图所示,已知△ABC中,PE∥AB交BC于E,PF∥AC交BC于F,P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.