题目内容
7.化简:(1)$\frac{12}{{m}^{2}-9}-\frac{2}{m-3}$
(2)($\frac{a}{a+2}+\frac{1}{{a}^{2}-4}$)$÷\frac{a-1}{a+2}$.
分析 (1)首先进行通分运算,进而合并分子化简即可;
(2)首先将括号里面进行通分运算,进而合并分子化简,再利用分式除法运算法则计算得出答案.
解答 解:(1)$\frac{12}{{m}^{2}-9}-\frac{2}{m-3}$
=$\frac{12}{(m-3)(m+3)}$-$\frac{2(m+3)}{(m-3)(m+3)}$
=$\frac{12-2m-6}{(m-3)(m+3)}$
=-$\frac{2}{m+3}$;
(2)($\frac{a}{a+2}+\frac{1}{{a}^{2}-4}$)$÷\frac{a-1}{a+2}$
=[$\frac{a(a-2)}{(a+2)(a-2)}$+$\frac{1}{(a-2)(a+2)}$]×$\frac{a+2}{a-1}$
=$\frac{(a-1)^{2}}{(a+2)(a-2)}$×$\frac{a+2}{a-1}$
=$\frac{a-1}{a-2}$.
点评 此题主要考查了分式的混合运算,正确进行分式的通分运算是解题关键.

练习册系列答案
相关题目
12.小华应选择( )统计图,表示优、良、及格的人数占班级人数的百分比.
| A. | 条形 | B. | 折线 | C. | 复式折线 | D. | 扇形 |

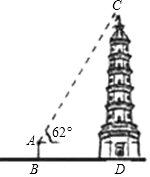 如图所示,位于昆明市昙华市内的瑞应塔,被誉为云南第一塔,某校九年级数学课外活动小组的同学准备利用假期测量超然楼的高度,甲同学在距离塔底部25m的B处地塔顶C的仰角为62°,若甲同学的眼睛到地面的高度AB为176cm,求瑞应塔C的高度(结果精确到0.1m,参考数据sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
如图所示,位于昆明市昙华市内的瑞应塔,被誉为云南第一塔,某校九年级数学课外活动小组的同学准备利用假期测量超然楼的高度,甲同学在距离塔底部25m的B处地塔顶C的仰角为62°,若甲同学的眼睛到地面的高度AB为176cm,求瑞应塔C的高度(结果精确到0.1m,参考数据sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)