题目内容
计算：
（1）3c3-2c2+8c-13c3+2c-2c2+3
（2）8x2-4（2x2+3x-1）
（3）5x2-2（3y2-5x2）+（-4y2+7xy）．
（1）3c3-2c2+8c-13c3+2c-2c2+3
（2）8x2-4（2x2+3x-1）
（3）5x2-2（3y2-5x2）+（-4y2+7xy）．
考点：整式的加减
专题：
分析：（1）直接合并同类项即可；
（2）（3）先去括号，再进一步合并同类项即可．
（2）（3）先去括号，再进一步合并同类项即可．
解答：解：（1）原式=-10c3-4c2+10c+3；
（2）原式=8x2-8x2-12x+4
=-12x+4；
（3）原式=5x2-6y2+10x2-4y2+7xy
=15x2-10y2+7xy．
（2）原式=8x2-8x2-12x+4
=-12x+4；
（3）原式=5x2-6y2+10x2-4y2+7xy
=15x2-10y2+7xy．
点评：此题考查整式的加减混合运算，掌握去括号的法则与积合并同类项的方法是解决问题的关键．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
三角形两边长分别为4和8，第三边是方程x2-8x+12=0的解，则这个三角形的周长是（ ）
| A、14 | B、18 |
| C、14和18 | D、14或18 |
用配方法解方程x2+6x+7=0，则方程可变为（ ）
| A、（x-3）2=2 |
| B、（x+3）2=2 |
| C、（x-6）2=12 |
| D、（x+6）2=49 |
解方程3-
=1，在下列去分母运算中，正确的是（ ）
| x+2 |
| 3 |
| A、3-（x+2）=3 |
| B、9-x-2=1 |
| C、9-（x+2）=3 |
| D、9-x+2=3 |
下列说法中正确的是（ ）
| A、在有理数中，零的意义仅表示没有 |
| B、一个数不是负数就是正数 |
| C、正有理数和负有理数组成全体有理数 |
| D、零是整数 |
下列各式中：
，2x4-1，7a+b，-2，
，
多项式有（ ）
| abc |
| 2 |
| a+b |
| 2 |
| m+n |
| m |
| A、2个 | B、3个 | C、4个 | D、5个 |
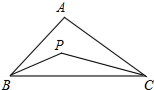已知：如图，在△ABC中，∠ABC，∠ACB的平分线相交于点P，
如图所示，直线BC经过原点O，点A在x轴上，AD⊥BC于D，若B（m，2），C（n，-3），A（2，0），则AD•BC=