题目内容
 如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.(1)若EF=3,BC=8,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.
考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:
分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得EM=FM=
BC,再根据三角形的周长公式列式计算即可得解;
(2)根据等腰三角形两底角相等求出∠BMF,∠CME,再根据平角等于180°列式计算即可得解.
| 1 |
| 2 |
(2)根据等腰三角形两底角相等求出∠BMF,∠CME,再根据平角等于180°列式计算即可得解.
解答:解:(1)∵CF⊥AB于F,BE⊥AC于E,M为BC的中点,
∴EM=FM=
BC=
×8=4,
∴△EFM的周长=4+4+3=11;
(2)∵CF⊥AB于F,BE⊥AC于E,M为BC的中点,
∴BM=MF=MC,
∵∠ABC=50°,∠ACB=60°,
∴∠BMF=180°-2×50°=80°,
∴∠CME=180°-2×60°=60°,
∴∠EMF=180°-80°-60°=40°.
∴EM=FM=
| 1 |
| 2 |
| 1 |
| 2 |
∴△EFM的周长=4+4+3=11;
(2)∵CF⊥AB于F,BE⊥AC于E,M为BC的中点,
∴BM=MF=MC,
∵∠ABC=50°,∠ACB=60°,
∴∠BMF=180°-2×50°=80°,
∴∠CME=180°-2×60°=60°,
∴∠EMF=180°-80°-60°=40°.
点评:本题考查了等腰三角形的性质,直角三角形斜边上的中线等于斜边的一半的性质,熟记性质是解题的关键.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
解方程3-
=1,在下列去分母运算中,正确的是( )
| x+2 |
| 3 |
| A、3-(x+2)=3 |
| B、9-x-2=1 |
| C、9-(x+2)=3 |
| D、9-x+2=3 |
下列各式中:
,2x4-1,7a+b,-2,
,
多项式有( )
| abc |
| 2 |
| a+b |
| 2 |
| m+n |
| m |
| A、2个 | B、3个 | C、4个 | D、5个 |
 已知⊙O中弦AB、CD相交于点P,PO平分∠APD,则下列结论中不正确的是( )
已知⊙O中弦AB、CD相交于点P,PO平分∠APD,则下列结论中不正确的是( )| A、AB=CD | ||||
B、
| ||||
| C、PA=PD | ||||
D、
|

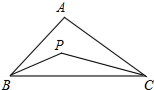 已知:如图,在△ABC中,∠ABC,∠ACB的平分线相交于点P,
已知:如图,在△ABC中,∠ABC,∠ACB的平分线相交于点P, 如图,△ADE∽△ACB,则DE:BC=
如图,△ADE∽△ACB,则DE:BC= 如图,CD是Rt△ABC斜边上的高.
如图,CD是Rt△ABC斜边上的高.