题目内容
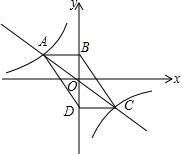 如图,A、C是双曲线上关于原点O对称的任意两点,AB垂直y轴于B,CD垂直y轴于D,且四边形ABCD的面积为6,则这个函数的解析式为
如图,A、C是双曲线上关于原点O对称的任意两点,AB垂直y轴于B,CD垂直y轴于D,且四边形ABCD的面积为6,则这个函数的解析式为考点:反比例函数系数k的几何意义,反比例函数图象上点的坐标特征
专题:计算题
分析:利用A、C关于原点O对称和AB垂直y轴于B,CD垂直y轴于D可得AB=CD,AB∥CD,于是可判断四边形ABCD为平行四边形,则S△AOB=
S四边形ABCD=
,设反比例函数的解析式为y=
,根据反比例函数系数k的几何意义得
|k|=
,然后去绝对值得到满足条件的k的值,从而得到反比例函数解析式.
| 1 |
| 4 |
| 3 |
| 2 |
| k |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:∵A、C是双曲线上关于原点O对称的任意两点,
而AB垂直y轴于B,CD垂直y轴于D,
∴AB=CD,AB∥CD,
∴四边形ABCD为平行四边形,
∴S△AOB=
S四边形ABCD=
×6=
,
设反比例函数的解析式为y=
,
∵
|k|=
,
而k<0,
∴k=-3,
∴反比例函数解析式为y=-
.
故答案为y=-
.
而AB垂直y轴于B,CD垂直y轴于D,
∴AB=CD,AB∥CD,
∴四边形ABCD为平行四边形,
∴S△AOB=
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
设反比例函数的解析式为y=
| k |
| x |
∵
| 1 |
| 2 |
| 3 |
| 2 |
而k<0,
∴k=-3,
∴反比例函数解析式为y=-
| 3 |
| x |
故答案为y=-
| 3 |
| x |
点评:本题考查了反比例函数系数k的几何意义:在反比例函数y=
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
| k |
| x |

练习册系列答案
相关题目
下列方程中是一元一次方程的是( )
A、x+4=
| ||
| B、3x+2y=1 | ||
| C、5x-1=2x2 | ||
| D、3+y=0 |
下列说法中正确的是( )
| A、在有理数中,零的意义仅表示没有 |
| B、一个数不是负数就是正数 |
| C、正有理数和负有理数组成全体有理数 |
| D、零是整数 |
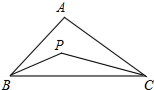 已知:如图,在△ABC中,∠ABC,∠ACB的平分线相交于点P,
已知:如图,在△ABC中,∠ABC,∠ACB的平分线相交于点P,
 如图,在⊙O中,
如图,在⊙O中,
