题目内容
5.若$\frac{y}{x-y}=\frac{5}{3}$,则$\frac{x}{y}$=8:5;$\frac{x-2y}{2x+y}$=$-\frac{2}{21}$.分析 根据比例的性质得出x:y=8:5,代入解答即可.
解答 解:由$\frac{y}{x-y}=\frac{5}{3}$,
变形为:3y=5x-5y,
解得:x:y=8:5,
把x:y=8:5变形为:x=$\frac{8}{5}$y,
把x=$\frac{8}{5}$y代入$\frac{x-2y}{2x+y}$=$\frac{\frac{8}{5}y-2y}{2×\frac{8}{5}y+y}=-\frac{2}{21}$,
故答案为:8:5;$-\frac{2}{21}$.
点评 此题考查比例的性质,关键是内项之积等于外项之积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列有理数的大小比较,正确的是( )
| A. | -5>0.1 | B. | 0>$\frac{1}{5}$ | C. | -5.1<-4.2 | D. | 0<$-\frac{1}{4}$ |
15.若(a2+b2-1)2=16,则a2+b2的值为( )
| A. | 5 | B. | -3 | C. | -3或5 | D. | -7或9 |
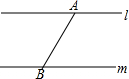 如图,已知两条平行直线l、m之间的距离为$\sqrt{3}$,A是直线l上一点,B是直线m上一点,AB=2,若点C在直线m上,且AC=3,则BC的长为1.
如图,已知两条平行直线l、m之间的距离为$\sqrt{3}$,A是直线l上一点,B是直线m上一点,AB=2,若点C在直线m上,且AC=3,则BC的长为1. 如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数$y=\frac{n}{x}$的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数$y=\frac{n}{x}$的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.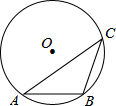 如图,在半径为5的⊙O中,弦AB=4,点C是优弧AB上一点(不与A、B重合),则sinC的值为$\frac{2}{5}$.
如图,在半径为5的⊙O中,弦AB=4,点C是优弧AB上一点(不与A、B重合),则sinC的值为$\frac{2}{5}$. 已知:线段a,∠α.
已知:线段a,∠α.