题目内容
17.如图1,定义:在四边形ABCD中,若AD=BC,且∠ADB+∠BCA=180°,则把四边形ABCD叫做互补等对边四边形,如图2,在等腰△ABE中,AE=BE,四边形ABCD是互补等对边四边形,求证:∠ABD=∠BAC=$\frac{1}{2}$∠E.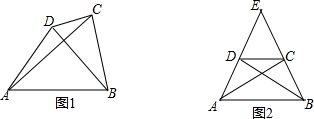
分析 根据等边对等角可得∠EAB=∠EBA,根据四边形ABCD是互补等对边四边形,可得AD=BC,根据SAS可证△ABD≌△BAC,根据全等三角形的性质可得∠ABD=∠BAC,再根据等腰三角形的性质即可证明.
解答 证明:∵AE=BE,
∴∠EAB=∠EBA,
∵四边形ABCD是互补等对边四边形,
∴AD=BC,
在△ABD与△BAC中,
$\left\{\begin{array}{l}{AD=BC}\\{∠EAB=∠EBA}\\{AB=BA}\end{array}\right.$,
∴△ABD≌△BAC(SAS),
∴∠ABD=∠BAC,∠ADB=∠BCA,
∵∠ADB+∠BCA=180°,
∴∠ADB=∠BCA=90°,
在等腰△ABE中,∠EAB=∠EBA=(180°-∠E)÷2=90°-$\frac{1}{2}$∠E,
∴∠ABD=90°-∠EAB=90°-(90°-$\frac{1}{2}$∠E)=$\frac{1}{2}$∠E,
∴∠ABD=∠BAC=$\frac{1}{2}$∠E.
点评 考查了等腰三角形的性质,全等三角形的判定和性质,关键是根据SAS证明△ABD≌△BAC.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.某校人数相等的甲、乙两个班同时进行测验,班级的平均分和方差分别为:$\overline{{x}_{甲}}$=78分,$\overline{{x}_{乙}}$=78分,s甲2=180,s乙2=80,那么成绩较为整齐的是( )
| A. | 甲班 | B. | 两个班一样整齐 | C. | 乙班 | D. | 无法确定 |
2.若a<b,则下列不等式中正确的是( )
| A. | 2a>2b | B. | a-b>0 | C. | -3a>-3b | D. | a-3<b-5 |
6.下列命题中正确的是( )
| A. | 有一组邻边相等的四边形是菱形 | |
| B. | 对角线互相垂直的平行四边形是正方形 | |
| C. | 有一个角是直角的平行四边形是矩形 | |
| D. | 一组对边平行的四边形是平行四边形 |
7.如表列出了一项实验的统计数据:
它表示皮球从一定高度落下时,下落高度y与弹跳高度x的关系,能表示变量y与x之间的关系式为( )
| y | 50 | 80 | 100 | 150 | … |
| x | 30 | 45 | 55 | 80 | … |
| A. | y=2x-10 | B. | y=x2 | C. | y=x+25 | D. | y=x+5 |
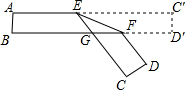 把一张两组对边分别平行的纸条折叠,如图所示,EF是折痕,若∠EFB=34°,则∠BFD度数为112°.
把一张两组对边分别平行的纸条折叠,如图所示,EF是折痕,若∠EFB=34°,则∠BFD度数为112°.
 如图,△ABC绕顶点A逆时针旋转35°至△ADE,∠B=40°,∠DAC=55°.求∠E的度数.
如图,△ABC绕顶点A逆时针旋转35°至△ADE,∠B=40°,∠DAC=55°.求∠E的度数.