题目内容
14.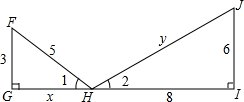 根据图中所注的条件,判断图中两个三角形是否相似,并求出x的值.
根据图中所注的条件,判断图中两个三角形是否相似,并求出x的值.
分析 由∠G=∠I=90°,直接利用勾股定理即可求得x与y的值,然后利用三组对应边的比相等的两个三角形相似证得结论.
解答 解:相似.
∵∠G=∠I=90°,
∴x=GH=$\sqrt{F{H}^{2}-F{G}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,y=HJ=$\sqrt{H{I}^{2}+I{J}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴$\frac{FG}{IJ}=\frac{GH}{HI}=\frac{FH}{HJ}$=$\frac{1}{2}$,
∴△FGH∽△JIH.
点评 此题考查了相似三角形的判定与勾股定理.注意掌握相似三角形的判定定理是关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
5. 如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
 如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )| A. | 10° | B. | 15° | C. | 25° | D. | 35° |
19. 某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读教科书情况统计图表
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2500名,请估计该校“重视阅读教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读教科书的现状的看法及建议;
②如果要了解全省初中生阅读教科书的情况,你认为应该如何进行抽样?
 某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:某校初中生阅读教科书情况统计图表
| 类别 | 人数 | 占总人数比例 |
| 重视 | a | b |
| 一般 | 57 | 0.285 |
| 不重视 | c | 0.36 |
| 说不清楚 | 9 | 0.045 |
(2)若该校共有初中生2500名,请估计该校“重视阅读教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读教科书的现状的看法及建议;
②如果要了解全省初中生阅读教科书的情况,你认为应该如何进行抽样?
6.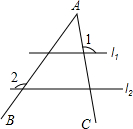 如图,∠A被平行直线l1、l2所截,若∠1=100°,∠2=125°,则∠A的度数是( )
如图,∠A被平行直线l1、l2所截,若∠1=100°,∠2=125°,则∠A的度数是( )
 如图,∠A被平行直线l1、l2所截,若∠1=100°,∠2=125°,则∠A的度数是( )
如图,∠A被平行直线l1、l2所截,若∠1=100°,∠2=125°,则∠A的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 45° |
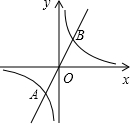 如图,已知正比例函数y=ax(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点为A(-1,2-k2),另一个交点为B,且A,B关于原点O对称.
如图,已知正比例函数y=ax(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点为A(-1,2-k2),另一个交点为B,且A,B关于原点O对称.