题目内容
 如图,BO、CO分别平分∠ABC、∠ACB,且∠BOC=110°,则∠A=
如图,BO、CO分别平分∠ABC、∠ACB,且∠BOC=110°,则∠A=考点:三角形内角和定理
专题:计算题
分析:先根据角平分线的定义得到∠OBC=
∠ABC,∠OCB=
∠ACB,再根据三角形内角和定理得∠BOC+∠OBC+∠OCB=180°,则∠BOC=180°-
(∠ABC+∠ACB),由于∠ABC+∠ACB=180°-∠A,所以∠BOC=90°+
∠A,然后把∠BOC=110°代入计算可得到∠A的度数.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
而∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-
(∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-∠A,
∴∠BOC=180°-
(180°-∠A)=90°+
∠A,
而∠BOC=110°,
∴90°+
∠A=110°
∴∠A=40°.
故答案为40°.
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
而∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-
| 1 |
| 2 |
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-∠A,
∴∠BOC=180°-
| 1 |
| 2 |
| 1 |
| 2 |
而∠BOC=110°,
∴90°+
| 1 |
| 2 |
∴∠A=40°.
故答案为40°.
点评:本题考查了三角形内角和定理:三角形内角和是180°.

练习册系列答案
相关题目
下列调查中,适宜采用抽样调查方式的是( )
| A、调查我市中学生每天体育锻炼的时间 |
| B、调查某班学生对“党的群众路线”的知晓率 |
| C、调查一架“歼20”隐形战机各零部件的质量 |
| D、调查广州亚运会100米参赛运动员兴奋剂的使用情况 |
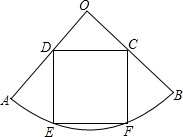 如图,扇形AOB的圆心角∠AOB=90°,半径为5,正方形CDEF内接于该扇形,则正方形CDEF的边长为
如图,扇形AOB的圆心角∠AOB=90°,半径为5,正方形CDEF内接于该扇形,则正方形CDEF的边长为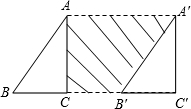 如图,∠C=90°,将直角三角形ABC沿着射线BC方向平移5cm,得三角形A′B′C′,已知BC=3cm,AC=4cm,则阴影部分的面积为
如图,∠C=90°,将直角三角形ABC沿着射线BC方向平移5cm,得三角形A′B′C′,已知BC=3cm,AC=4cm,则阴影部分的面积为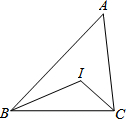 如图,△ABC中,点I是∠ABC、∠ACB角平分线的交点,∠BIC=130°,则∠A=
如图,△ABC中,点I是∠ABC、∠ACB角平分线的交点,∠BIC=130°,则∠A=