题目内容
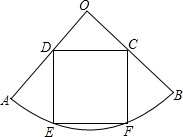 如图,扇形AOB的圆心角∠AOB=90°,半径为5,正方形CDEF内接于该扇形,则正方形CDEF的边长为
如图,扇形AOB的圆心角∠AOB=90°,半径为5,正方形CDEF内接于该扇形,则正方形CDEF的边长为考点:勾股定理,等腰直角三角形,正方形的性质
专题:
分析:过O作OG⊥EF,交CD于点H,连接OE.设DH=a,根据正方形的性质和等腰直角三角形的性质可得OG=3a,在Rt△OEG中,根据勾股定理可得a的值,进一步得到正方形CDEF的边长为
解答: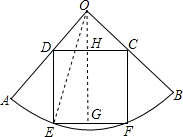 解:过O作OG⊥EF,交CD于点H,连接OE,
解:过O作OG⊥EF,交CD于点H,连接OE,
设DH=a,
∵四边形CDEF是正方形,
∴OH⊥CD,△OCD是等腰直角三角形,
∴CH=DH=a,
∵∠AOC=90°,
∴CH=OH,
∴OG=3a,
在Rt△OEG中,
OE2=GE2+OG2,即52=a2+(3a)2,
解得a=
,
∴CF=2a=
.
故正方形CDEF的边长为
.
故答案为:
.
 解:过O作OG⊥EF,交CD于点H,连接OE,
解:过O作OG⊥EF,交CD于点H,连接OE,设DH=a,
∵四边形CDEF是正方形,
∴OH⊥CD,△OCD是等腰直角三角形,
∴CH=DH=a,
∵∠AOC=90°,
∴CH=OH,
∴OG=3a,
在Rt△OEG中,
OE2=GE2+OG2,即52=a2+(3a)2,
解得a=
| ||
| 2 |
∴CF=2a=
| 10 |
故正方形CDEF的边长为
| 10 |
故答案为:
| 10 |
点评:本题考查的是垂径定理及勾股定理,解答此题的关键是根据题意画出图形,作出辅助线,构造出直角三角形,再进行解答.

练习册系列答案
相关题目
 张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.汽车到达乙地时油箱中还余油
张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.汽车到达乙地时油箱中还余油 如图,BO、CO分别平分∠ABC、∠ACB,且∠BOC=110°,则∠A=
如图,BO、CO分别平分∠ABC、∠ACB,且∠BOC=110°,则∠A=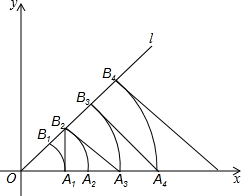 如图,已知直线l的表达式为y=x,点A1的坐标为(1,0),以O为圆心,OA1为半径画弧,与直线l交于点B1,过点A1作x轴的垂线交直线l于点B2,以O为圆心,OB2为半径画弧,交x轴于A2;过点B2作直线l的垂线交x轴于点A3,以O为圆心,OA3为半径画弧,交直线l于B3;过点B3作直线,的垂线交x轴于点A4,以O为圆心,OA4为半径画弧,交直线l于B4,过点B4作直线l的垂线交x轴于点A5…按照这样规律进行下去,点B2014的坐标为
如图,已知直线l的表达式为y=x,点A1的坐标为(1,0),以O为圆心,OA1为半径画弧,与直线l交于点B1,过点A1作x轴的垂线交直线l于点B2,以O为圆心,OB2为半径画弧,交x轴于A2;过点B2作直线l的垂线交x轴于点A3,以O为圆心,OA3为半径画弧,交直线l于B3;过点B3作直线,的垂线交x轴于点A4,以O为圆心,OA4为半径画弧,交直线l于B4,过点B4作直线l的垂线交x轴于点A5…按照这样规律进行下去,点B2014的坐标为