题目内容
20. 如图,将纸片△ABC沿着DE折叠压平,用∠1、∠2来表示∠A.
如图,将纸片△ABC沿着DE折叠压平,用∠1、∠2来表示∠A.
分析 由折叠及邻补角的性质可知,∠1=180°-2∠ADE,∠2=180°-2∠AED,两式相加,结合已知可求∠ADE+∠AED的度数,在△ADE中,由内角和定理可求∠A的度数.
解答 解:根据折叠及邻补角的性质,得
∠1=180°-2∠ADE,∠2=180°-2∠AED,
∴∠1+∠2=360°-2(∠ADE+∠AED),
∴∠ADE+∠AED=$\frac{1}{2}$[360°-(∠1+∠2)]=180°-$\frac{1}{2}$(∠1+∠2),
∴在△ADE中,由内角和定理,得
∠A=180°-(∠ADE+∠AED)=180°-180°+$\frac{1}{2}$(∠1+∠2)=$\frac{1}{2}$(∠1+∠2).
点评 本题考查了折叠的性质,邻补角的性质,三角形内角和定理,关键是把∠1+∠2看作整体,对角的和进行转化.

练习册系列答案
相关题目
10.若抛物线的最高点的纵坐标是$\frac{25}{4}$,且过点(-1,0),(4,0),则该抛物线的解析式为( )
| A. | y=-x2+3x+4 | B. | y=-x2-3x+4 | C. | y=x2-3x-4 | D. | y=x2-3x+4 |
 如图所示的一个魔方(正方体),每个面都是由9个面积为4cm2的小正方形拼成,求这个魔方的棱长.
如图所示的一个魔方(正方体),每个面都是由9个面积为4cm2的小正方形拼成,求这个魔方的棱长.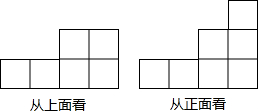 由一些大小相同的小正方体组成的简单几何体从正面和上面看到的平面图形如图所示.
由一些大小相同的小正方体组成的简单几何体从正面和上面看到的平面图形如图所示.