题目内容
2．四条线段的长分别为4，5，6，7，则它们首尾相连可以组成不同的三角形的个数是（ ）| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
分析 首先写出所有的组合可能，然后根据三角形的三边关系进行分析．
解答 解：其中的任意三条组合有4、5、6；5、6、7；4、6、7；4、5、7四种情况．
根据三角形的三边关系，知都能组成三角形．
故选A．
点评 此题主要考查了三角形的三边关系．三角形的任意两边之和大于第三边，任意两边之差小于第三边．
练习册系列答案
相关题目
13．下面关于函数的三种表示方法叙述错误的是（ ）
| A． | 用图象法表示函数关系，可以直观地看出因变量如何随着自变量而变化 | |
| B． | 用列表法表示函数关系，可以很清楚地看出自变量取的值与因变量的对应值 | |
| C． | 用公式法表示函数关系，可以方便地计算函数值 | |
| D． | 任何函数关系都可以用上述三种方法来表示 |
10．如图：在△ABC中，∠ACB=90°，∠B=30°，AC=1，AC在直线l上，将△ABC绕点A顺时针旋转到位置①，可得到点P1，此时AP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=2+$\sqrt{3}$；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，可得到点P3，此时AP3=3+$\sqrt{3}$；…，按此规律继续旋转，直到得到点P2015为止，则AP2015=（ ）
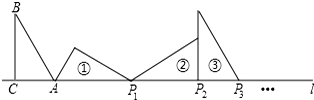
| A． | 2015+672$\sqrt{3}$ | B． | 2013+671$\sqrt{3}$ | C． | 2013+672$\sqrt{3}$ | D． | 2015+671$\sqrt{3}$ |