题目内容
16.下列方程中,有两个不等实数根的是( )| A. | x2+1=0 | B. | x2+2x+1=0 | C. | x2+x-1=0 | D. | ax2+bx+c=0 |
分析 分别套入数据求取四个选项的b2-4ac的值,由此即可得出结论.
解答 解:A、b2-4ac=0-4×1×1=-4<0,
该方程无实数根;
B、b2-4ac=4-4×1×1=0,
该方程有两个相等的实数根;
C、b2-4ac=1-4×(-1)×1=5>,
该方程有两个不相等的实数根;
D、b2-4ac无法判断其符号.
故选C.
点评 本题考查了根的判别式,解题的关键是分别求出四个选项中b2-4ac的值.本题属于基础题,难度不大,解决该题型题目时,根据根的判别式的符号判断根的个数是关键.

练习册系列答案
相关题目
4.下列计算正确的是( )
| A. | (2x-1)(x+1)=2x2-1 | B. | (a-3b)2=a2-9b2 | ||
| C. | (x+5)(x-2)=x2-3x-10 | D. | (-3+2a)2=9-12a+4a2 |
11.将甲乙两数据进行比较,如果甲的波动性大,那么( )
| A. | 甲的标准差小 | B. | 乙的方差小 | C. | 甲的平均数大 | D. | 乙的中位数小 |
8. 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )| A. | 10$\sqrt{3}$+1 | B. | 10$\sqrt{3}$ | C. | 10.5 | D. | 11.5 |
6.已知△ABC中,求作一点P,使P到∠A的两边的距离相等,且PB=PC,则下列确定P点的方法正确的是( )
| A. | P是∠A与∠B两角平分线的交点 | |
| B. | P是AC、AB两边上中垂线的交点 | |
| C. | P是∠A的角平分线与BC的中垂线的交点 | |
| D. | P是∠A的角平分线与AB的中垂线的交点 |
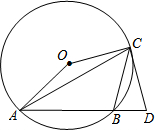 如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.
如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.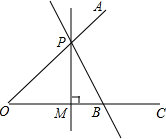 画图并回答问题.
画图并回答问题.