题目内容
15.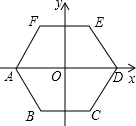 如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若D点的坐标为(2,0),则点F的坐标为( )
如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若D点的坐标为(2,0),则点F的坐标为( )| A. | (-1,$\sqrt{3}$) | B. | (-$\sqrt{3}$,1) | C. | (-$\sqrt{3}$,$\sqrt{3}$) | D. | (-1,1) |
分析 先连接OF,由于正六边形是轴对称图形,并设EF交y轴于G,那么∠GOF=30°;在Rt△GOF中,则GF=1,OG=$\sqrt{3}$.即可求得E的坐标.
解答 解:连接OF,如图所示
由正六边形是轴对称图形知:
在Rt△OFG中,∠GOF=30°,OF=2.
∴GF=1,OG=$\sqrt{3}$,
∴F(-1,$\sqrt{3}$),
故选:A.
点评 本题利用了正六边形的对称性,直角三角形30°的角所对的边等于斜边的一半,勾股定理等知识,求出GF和OG的长是关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
6.a6÷a3结果是( )
| A. | a3 | B. | a2 | C. | a9 | D. | a-3 |
3.下列计算正确的是( )
| A. | 2x+1=2x2 | B. | x2•x3=x5 | C. | (x2)3=x5 | D. | (2x)3=2x3 |
20.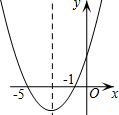 如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2-4ac>0;④a+b+c<0;⑤对于图象上的两点(-6,m )、(1,n),有m<n.其中正确信息的个数有( )
如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2-4ac>0;④a+b+c<0;⑤对于图象上的两点(-6,m )、(1,n),有m<n.其中正确信息的个数有( )
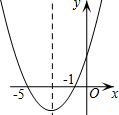 如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2-4ac>0;④a+b+c<0;⑤对于图象上的两点(-6,m )、(1,n),有m<n.其中正确信息的个数有( )
如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2-4ac>0;④a+b+c<0;⑤对于图象上的两点(-6,m )、(1,n),有m<n.其中正确信息的个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
7.下列计算中,正确的是( )
| A. | -a(3a2-1)=-3a3-a | B. | (-2a-3)(2a-3)=9-4a2 | ||
| C. | (2+x)(x-2)=4-x2 | D. | (ab-c)(-c+ab)=a2b2-c2 |
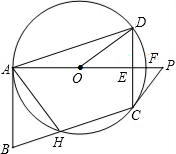 如图,⊙O过?ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AP交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
如图,⊙O过?ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AP交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF. 如图,△ABC的边BC长是8,BC边上的高AD′是4,点D在BC运动,设BD长为x,请写出△ACD的面积y与x之间的函数关系式y=-2x+16.
如图,△ABC的边BC长是8,BC边上的高AD′是4,点D在BC运动,设BD长为x,请写出△ACD的面积y与x之间的函数关系式y=-2x+16.