题目内容
4．
如图，△ABC的边BC长是8，BC边上的高AD′是4，点D在BC运动，设BD长为x，请写出△ACD的面积y与x之间的函数关系式y=-2x+16．
分析 直接利用三角形面积求法得出y与x之间的函数关系即可．
解答 解：由题意可得，△ACD的面积y与x之间的函数关系式为：
y=$\frac{1}{2}$AD′•DC=$\frac{1}{2}$×4×（8-x）=-2x+16．
故答案为：y=-2x+16．
点评 此题主要考查了函数关系式，正确掌握钝角三角形面积求法是解题关键．
练习册系列答案
口算能手系列答案
相关题目
15．
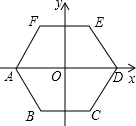如图，将正六边形ABCDEF放在直角坐标系中，中心与坐标原点重合，若D点的坐标为（2，0），则点F的坐标为（ ）
如图，将正六边形ABCDEF放在直角坐标系中，中心与坐标原点重合，若D点的坐标为（2，0），则点F的坐标为（ ）| A． | （-1，$\sqrt{3}$） | B． | （-$\sqrt{3}$，1） | C． | （-$\sqrt{3}$，$\sqrt{3}$） | D． | （-1，1） |
12．若点P1（x1，x2），P（x2，y2）在反比例函数y=$\frac{k}{x}$（k＞0）的图象上，且x1＜x2，则（ ）
| A． | y1＜y2 | B． | y1＞y2 | C． | y1=y2 | D． | 以上都不对 |
19．下列运算中，正确的是（ ）
| A． | 3a+2b=5ab | B． | 2a3+3a2=5a5 | C． | 5a2-4a2=1 | D． | 5a2b-5ba2=0 |
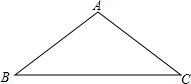如图，在△ABC中，AB=AC=10，BC=16．
如图，点C是AB为直径的半圆上一点（O为圆心），以AC、BC为边向上作正方形ACDE和正方形ECFG，点P是DF的中点，若OP=6$\sqrt{2}$，AB=10，则△ABC的面积为多少？
如图，在正方形ABCD中，点E是AD上的点，点F是BC的延长线一点，CF=DE，连结BE和EF，EF与CD交于点G，且∠FBE=∠FEB．