题目内容
二次函数y=ax2+bx-3中x、y满足下表:
(1)求这个二次函数的解析式;
(2)求m=?
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -3 | -4 | -3 | m | … |
(2)求m=?
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征
专题:
分析:(1)找一组点的坐标代入抛物线的解析式即可求出a、b值,进而求得解析式.
(2)把x=3代入(1)中的解析式即可求得m的值;
(2)把x=3代入(1)中的解析式即可求得m的值;
解答:解:(1)由题意得(-1,0),(1,-4)在二次函数y=ax2+bx-3图象上
∴
,
解得:a=1,b=-2,
∴这个二次函数的解析式为y=x2-2x-3.
(2)当x=3时,y=x2-2x-3=9-6-3=0.
∴m=0.
∴
|
解得:a=1,b=-2,
∴这个二次函数的解析式为y=x2-2x-3.
(2)当x=3时,y=x2-2x-3=9-6-3=0.
∴m=0.
点评:考查了用待定系数法求二次函数解析式的方法.本题中要求熟练掌握二次函数的基本性质.

练习册系列答案
相关题目
已知二次函数y=(2x-1)2-2,其顶点坐标是( )
| A、(1,-2) | ||
B、(
| ||
C、(-
| ||
| D、(-1,-2) |
 如图,△ABC中,AD⊥BC,垂足是D.若BC=14,AD=12,tan∠BAD=
如图,△ABC中,AD⊥BC,垂足是D.若BC=14,AD=12,tan∠BAD=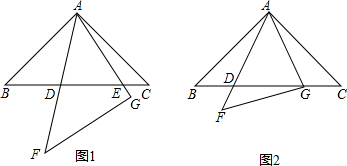
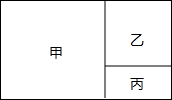 如图,是我市一块长方形土地,政府统一规划,把地分成甲、乙、丙三部分,甲和乙为正方形,现计划甲建设住宅区,乙建设一座标准化的中学,丙地建成植物园,若已知这块地的宽为120米,丙地的面积为3200平方米,请你计算出这块地的长是多少?
如图,是我市一块长方形土地,政府统一规划,把地分成甲、乙、丙三部分,甲和乙为正方形,现计划甲建设住宅区,乙建设一座标准化的中学,丙地建成植物园,若已知这块地的宽为120米,丙地的面积为3200平方米,请你计算出这块地的长是多少?