题目内容
若一个两位正整数m的个位数为8,则称m为“好数”.
(1)求证:对任意“好数”m,m2-64一定为20的倍数;
(2)若m=p2-q2,且p,q为正整数,则称数对(p,q)为“友好数对”,规定: 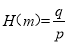 ,例如68=182-162,称数对(18,16)为“友好数对”,则
,例如68=182-162,称数对(18,16)为“友好数对”,则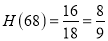 ,求小于50的“好数”中,所有“友好数对”的H(m)的最大值.
,求小于50的“好数”中,所有“友好数对”的H(m)的最大值.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
若一个两位正整数m的个位数为8,则称m为“好数”.
(1)求证:对任意“好数”m,m2-64一定为20的倍数;
(2)若m=p2-q2,且p,q为正整数,则称数对(p,q)为“友好数对”,规定: 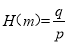 ,例如68=182-162,称数对(18,16)为“友好数对”,则
,例如68=182-162,称数对(18,16)为“友好数对”,则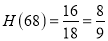 ,求小于50的“好数”中,所有“友好数对”的H(m)的最大值.
,求小于50的“好数”中,所有“友好数对”的H(m)的最大值.
 阅读快车系列答案
阅读快车系列答案