题目内容
 如图,在正方形网格上有相似三角形△A1B1C1和△A2B2C2,则△A1B1C1和△A2B2C2的面积比为( )
如图,在正方形网格上有相似三角形△A1B1C1和△A2B2C2,则△A1B1C1和△A2B2C2的面积比为( )| A、2 | ||
B、
| ||
| C、4 | ||
D、
|
考点:相似三角形的性质
专题:
分析:观察图形求出两三角形的相似比,再根据相似三角形的面积的比等于相似比的平方解答.
解答:解:由图可知,△A1B1C1和△A2B2C2的相似比为2,
所以,△A1B1C1和△A2B2C2的面积比4.
故选C.
所以,△A1B1C1和△A2B2C2的面积比4.
故选C.
点评:本题考查了相似三角形的性质,熟记性质是解题的关键,难点在于观察出相似比.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
用语言叙述
-3表示的数量关系中,表述不正确的是( )
| 1 |
| x |
| A、比x的倒数小3 |
| B、比x倒数大3的数 |
| C、x的倒数与3的差 |
| D、1除以x的商与3的差 |
八年级某班50名学生的年龄统计结果如表所示,则此班学生年龄数据的众数、中位数分别为( )
| 年龄 | 13 | 14 | 15 | 16 |
| 人数 | 6 | 20 | 21 | 3 |
| A、14,14 |
| B、15,14 |
| C、14,15 |
| D、15,16 |
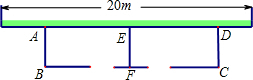 如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米.
如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米. 如图所示,AC垂直BC于C,AD垂直BD于D,AD=BC,CE垂直AB,DF垂直AB,垂足分别是E,F.求证:△BCE≌△ADF.
如图所示,AC垂直BC于C,AD垂直BD于D,AD=BC,CE垂直AB,DF垂直AB,垂足分别是E,F.求证:△BCE≌△ADF.